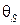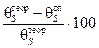Результаты испытания и оформление отчета
1. Вычитая из последующего значения предыдущее в колонках F, n 1, n 2, n 3, n 4, n 5, n 6, n 7, n 8 таблицы опытных данных, вычислить приращение нагрузки D F и приращения показания стрелочных тензометров D n 1, D n 2, D n 3, D n 4, D n 5, D n 6, D n 7, D n 8.
2. Построить графики зависимостей прогибов балки от нагрузки. Учитывая, что прогибы балки пропорциональны показаниям стрелочных тензометров, на вертикальной оси откладывать сумму приращений показаний прибора SD ni. На горизонтальной оси откладывать сумму приращений нагрузки SD Fi. Полученные точки соединить прямыми штриховыми отрезками, а затем провести сплошные прямые так, чтобы отклонения опытных точек были минимальными. Из графиков (рис. 27) очевидно, что зависимости прогибов балки от нагрузки действительно близки к прямым линиям. Поэтому делаем вывод о том, что закон Гука выполняется. Вблизи середины пролета (в точке S) прогиб направлен вниз, а на консоли (в точке D) – направлен вверх.
3. Вычислить средние арифметические значения приращений нагрузки D Fm и средние значения приращений показаний приборов D n 1 m, D n 2 m, D n 3 m, D n 4 m, D n 5 m, D n 6 m, D n 7 m, D n 8 m и записать их в соответствующие позиции таблицы опытных данных.
где i – номер прибора; m – обозначение среднего значения; k – номер ступени загружения; M – количество ступеней загружения; N – количество измерительных приборов. 4. Вычислить средние значения углов поворота сечений на одной ступени нагружения на левой опоре балки и в ее пролете. Так как углы поворота сечений малы по сравнению с единицей, то справедливо приближенное равенство (рис. 28)
где u в, u н – горизонтальные перемещения, соответственно, верхней и нижней точек стержня 13;
d – расстояние между верхним и нижним приборами на стержне 13.
5. Вычислить перемещение произвольной точки балки за счет осадок опор, предполагая, что балка остается прямолинейной. Согласно рисунку 29, получим выражение
Задавая соответствующие значения координате z, вычислить перемещения в точках S и D.
6. Вычислим опытные перемещения, включающие перемещения, вызванные деформациями опор балки
7. Вычислить прогибы балки, то есть перемещения, вызванные только ее искривлением
8. Вычислить относительные прогибы в расчетных точках балки 9. Вычислить реакции опор балки от среднего значения приращения нагрузки D F. Для этого следует использовать уравнения равновесия
10. Для определения прогибов балки и углов поворота ее расчетных сечений использовать метод начальных параметров. Составим универсальное уравнение упругой оси балки по расчетной схеме (рис. 30).
11. Определить начальные параметры универсального уравнения упругой изогнутой оси балки из условия ее закрепления. По условию закрепления балки на левой опоре A вычислим первый начальный параметр. При z = 0 прогиб должен быть равным нулю V = 0
Решение уравнения (85) дает значение EJV o = 0. Модуль упругости и осевой момент инерции поперечного сечения балки не равны нулю E ¹ 0 и J ¹ 0. Отсюда следует, что первый начальный параметр равен нулю V o = 0. По условию закрепления балки на правой опоре B определить второй начальный параметр. При z = a + b прогиб должен быть равен также нулю V = 0
Из полученного уравнения найти значение EJ qo и значение второго начального параметра qo. 12. Используя универсальное уравнение упругой оси балки (83) вычислить прогибы балки в расчетных точках S и D, задавая соответствующие значения координате z. 13. Используя уравнение для углов поворота (84) определить углы поворота сечения на опоре A и расчетного сечения S. 14. Сделать сравнение результатов, полученных испытанием балки и теоретическим расчетом в форме таблицы.
Расхождение в прогибах и углах поворота вычислить как отношение результатов, полученных опытным путем и теоретически, деленное на теоретический результат. Если знаменатель равен нулю, то расхождение не вычисляется и в соответствующей позиции таблицы ставится прочерк. 15. По полученным результатам сделать выводы. 16. Оформить отчет по лабораторной работе. Пример оформления отчета приведен в приложении.
Контрольные вопросы по разделу 13 1. Чем обусловлена необходимость требований по жесткости к изгибаемым элементам? 2. Какой метод использован в лабораторной работе для определения прогибов и углов поворота сечений балки? 3. Почему метод начальных параметров является приближенным методом расчета деформаций балок? 4. Какая цель ставится в лабораторной работе? 5. Какие требования предъявляются при испытании балки? 6. На какой установке проводится испытание на изгиб? 7. Что является объектом испытания на изгиб? 8. Как опирается балка? 9. Для чего служит спаренная швеллерная балка? 10. Для чего измеряются высота сечения двутавра и средняя толщина полки? 11. Какие измерительные инструменты используются при проведении лабораторной работы? 12. Какие приборы используются для определения прогибов и углов поворота сечений балки? 13. Чему равна цена деления стрелочного индикатора? 14. Как заполняется таблица опытных данных? 15. Как строятся графики зависимостей прогибов балки от нагрузки? 16. Какой вывод можно сделать по результатам анализа зависимости прогибов балки от нагрузки? 17. Как показания стрелочных тензометров, предназначенных для измерения линейных смещений, используются для определения углов поворота поперечных сечений балки? 18. Как вычисляются перемещения точек балки только за счет деформации опор? 19. По каким выражениям определяются опытные перемещения точек балки? 20. Как вычисляются опытные прогибы балки, то есть перемещения, вызванные только искривлением балки? 21. Как определяются реакции опор опытной балки? 22. Как составляются универсальное уравнение упругой оси балки и уравнение углов поворота ее поперечных сечений по методу начальных параметров? 23. По каким условиям определяются начальные параметры? 24. Как оценивается достоверность теории расчета тонких балок? 25. Какие выводы можно сделать по результатам исследований, проведенных в лабораторной работе?
ЛИТЕРАТУРА 1. Инструкция по охране труда / Разработана на кафедре сопротивления материалов и теории упругости. 2010 г. 2. Александров А.В. Сопротивление материалов/А.В.Александров, В.Д.Потапов, Б.П.Державин; под ред. А.В.Александрова. – М.: Высш. шк., 1995. –560 с. 3. Сопротивление материалов/А.Ф.Смирнов [и др.]; под общ. ред. А.Ф.Смирнова. – М.: Высш. шк., 1975. – 480 с. 4. Феодосьев В.И. Сопротивление материалов/В.И.Феодосьев. – М.: Наука, 1986. –560 с. 5. Сопротивление материалов (лабораторный практикум) / М.К.Балыкин, В.А.Пенькевич, В.Н.Заяц, И.А.Голубев. Минск, 1999 – 158 с 6. Справочник по сопротивлению материалов / Е.Ф.Винокуров [и др.]. – Минск: Наука и техника, 1988. – 464 с 7. Рубашкин А.П. Лабораторные работы по сопротивлению материалов. Учебное пособие. Изд. 3-е. М.,»Высшая школа», 1971. – 240 с. 8. Металловедение и технология металлов. Под ред. Ю.П.Солнцева. М., ”Металлургия”, 1988 – 512 с.
|


 ;
; 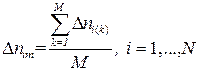 , (77)
, (77) , (78)
, (78) – среднее приращение показаний верхнего и нижнего приборов, установленных на стержне 13;
– среднее приращение показаний верхнего и нижнего приборов, установленных на стержне 13;

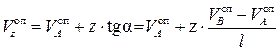 . (79)
. (79)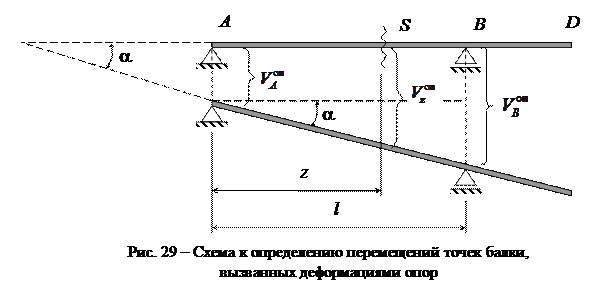
 (80)
(80) (81)
(81) и
и 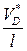
 (82)
(82)
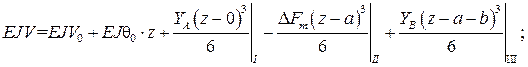 (83)
(83) (84)
(84) . (85)
. (85) . (86)
. (86)