Дискретная случайная переменная
Ваше интуитивное понимание вероятности почти наверняка соответствует задачам этой книги, и поэтому мы опустим традиционный раздел чистой теории вероятностей, хотя он мог бы быть весьма увлекательным. Многие люди непосредственно сталкивались с вероятностями, участвуя в лотереях и азартных играх, и их заинтересованность в том, чем они занимались, часто приводила к удивительно высокой практической компетентности, обычно при полном отсутствии формальной подготовки. Мы начнем непосредственно с дискретных случайных переменных. Случайная переменная – это любая переменная, значение которой не может быть точно предсказано. Дискретной называется случайная величина, имеющая определенный набор возможных значений. Пример – сумма выпавших очков при бросании двух игральных костей. Пример случайной величины, не являющейся дискретной, – температура в комнате. Она может принять любое из непрерывного диапазона значений и является примером непрерывной случайной величины. К рассмотрению таких величин в этом приложении мы перейдем позже. Продолжая разговор о примере с двумя игральными костями, предположим, что одна из них зеленая, а другая – красная. Если их бросить, то возможны 36 элементарных исходов эксперимента, поскольку на зеленой кости может выпасть любое число от 1 до 6 и то же самое – на красной. Случайная переменная, определенная как их сумма, которую мы обозначим через Таблица A.1
Предположив, что кости «правильные», мы можем воспользоваться табл. A.1 для определения вероятности каждого значения Таблица A.2
Совокупность всех возможных значений случайной переменной описывается генеральной совокупностью, из которой извлекаются эти значения. В нашем случае генеральная совокупность – это набор чисел от 2 до 12.
|

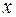 , может принимать только одно из 11 числовых значений — от 2 до 12. Взаимосвязь между исходами эксперимента и значениями случайной величины в данном случае показана в табл. A.1.
, может принимать только одно из 11 числовых значений — от 2 до 12. Взаимосвязь между исходами эксперимента и значениями случайной величины в данном случае показана в табл. A.1. равна 1/36. Чтобы получить сумму
равна 1/36. Чтобы получить сумму  , нам потребуются сочетания {зеленая=1, красная=6}, либо {зеленая=2, красная=5}, либо {зеленая=3, красная=4}, либо {зеленая=4, красная=3}, либо {зеленая=5, красная=2}, либо {зеленая=6, красная=1}. В данном случае нас устроят 6 возможных исходов, и поэтому вероятность получения 7 равна 6/36. Все эти вероятности приведены в табл. A.2. Если все их сложить, то получится ровно 1. Это будет так, поскольку с вероятностью 100% рассматриваемая сумма примет одно из значений от 2 до 12.
, нам потребуются сочетания {зеленая=1, красная=6}, либо {зеленая=2, красная=5}, либо {зеленая=3, красная=4}, либо {зеленая=4, красная=3}, либо {зеленая=5, красная=2}, либо {зеленая=6, красная=1}. В данном случае нас устроят 6 возможных исходов, и поэтому вероятность получения 7 равна 6/36. Все эти вероятности приведены в табл. A.2. Если все их сложить, то получится ровно 1. Это будет так, поскольку с вероятностью 100% рассматриваемая сумма примет одно из значений от 2 до 12.


