Правила расчета математического ожидания
Существуют три правила, которые часто используются. Эти правила практически самоочевидны, и они одинаково применимы для дискретных и непрерывных случайных переменных. Правило 1. Математическое ожидание суммы нескольких переменных равно сумме их математических ожиданий. Например, если имеются три случайные переменные
Правило 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если
Правило 3. Математическое ожидание константы есть она сама. Например, если
Следствие из трех правил:
Независимость случайных переменных Две случайные переменные
для любых функций
|

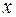 ,
,  и
и  , то
, то . (A.4)
. (A.4) – константа, то
– константа, то . (A.5)
. (A.5)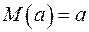 . (A.6)
. (A.6) .
. (A.7)
(A.7) и
и  . Из независимости следует как важный частный случай, что
. Из независимости следует как важный частный случай, что  .
.


