Постоянная и случайная составляющие случайной переменной
Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайную составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если
где Конечно, можно было бы посмотреть на это по-другому и сказать, что случайная составляющая
Из определения следует, что математическое ожидание величины
Поскольку весь разброс значений
и
Таким образом, Обобщая, можно утверждать, что если
|
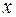– случайная переменная и 
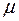– ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:
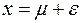, (A.14)
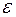– чисто случайная составляющая.
. (A.15)
.
.
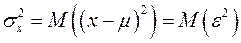
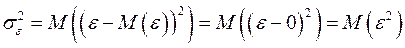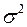может быть эквивалентно определена как дисперсия 
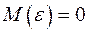и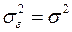 
, то математическое ожидание величины 
