Несмещенность
Поскольку оценки являются случайными переменными, их значения лишь по случайному совпадению могут в точности равняться характеристикам генеральной совокупности. Обычно будет присутствовать определенная ошибка, которая может быть большой или малой, положительной или отрицательной, в зависимости от чисто случайных составляющих величин Хотя это и неизбежно, на интуитивном уровне желательно, тем не менее, чтобы оценка в среднем за достаточно длительный период была аккуратной. Выражаясь формально, мы хотели бы, чтобы математическое ожидание оценки равнялось бы соответствующей характеристике генеральной совокупности. Если это так, то оценка называется несмещенной. Если это не так, то оценка называется смещенной, и разница между ее математическим ожиданием и соответствующей теоретической характеристикой генеральной совокупности называется смещением. Начнем с выборочного среднего. Является ли оно несмещенной оценкой теоретического среднего? Равны ли Величина
Тем не менее полученная оценка – не единственно возможная несмещенная оценка
Математическое ожидание
Если сумма Таким образом, в принципе число несмещенных оценок бесконечно. Как выбрать одну из них? Почему в действительности мы всегда используем выборочное среднее с До сих пор мы рассматривали только оценки теоретического среднего. Выше утверждалось, что величина
|

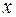 в выборке.
в выборке. и
и 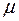 ? Да, это так, что непосредственно вытекает из (A.18).
? Да, это так, что непосредственно вытекает из (A.18).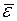 . Значение
. Значение 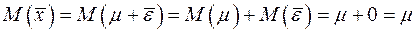 . (A.19)
. (A.19) и
и  . Любое взвешенное среднее наблюдений
. Любое взвешенное среднее наблюдений  . (A.20)
. (A.20) равно:
равно: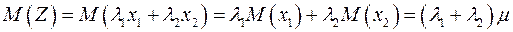 . (A.21)
. (A.21) и
и  равна единице, то мы имеем
равна единице, то мы имеем 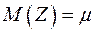 и
и  ? Возможно, вы полагаете, что было бы несправедливым давать разным наблюдениям различные веса или что подобной асимметрии следует избегать в принципе. Мы, однако, не заботимся здесь о справедливости или о симметрии как таковой. Дальше мы увидим, что имеется и более осязаемая причина.
? Возможно, вы полагаете, что было бы несправедливым давать разным наблюдениям различные веса или что подобной асимметрии следует избегать в принципе. Мы, однако, не заботимся здесь о справедливости или о симметрии как таковой. Дальше мы увидим, что имеется и более осязаемая причина.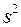 , определяемая в соответствии с табл. А.6, является оценкой теоретической дисперсии
, определяемая в соответствии с табл. А.6, является оценкой теоретической дисперсии 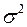 . Можно показать, что математическое ожидание
. Можно показать, что математическое ожидание 


