Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений 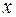 в выборке случайно, поскольку
в выборке случайно, поскольку 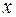 – случайная переменная и, следовательно, случайной величиной является и функция набора ее значений. Возьмем, например,
– случайная переменная и, следовательно, случайной величиной является и функция набора ее значений. Возьмем, например, 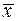 – оценку математического ожидания:
– оценку математического ожидания:
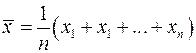 .
.
Выше мы показали, что величина 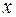 в
в  -м наблюдении может быть разложена на две составляющие: постоянную часть
-м наблюдении может быть разложена на две составляющие: постоянную часть 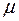 и чисто случайную составляющую
и чисто случайную составляющую 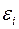 :
:
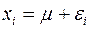 . (A.17)
. (A.17)
Следовательно,
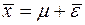 , (A.18)
, (A.18)
где 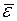 – выборочное среднее величин
– выборочное среднее величин 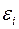 .
.
Отсюда можно видеть, что 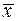 , подобно
, подобно 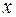 , имеет как фиксированную, так и чисто случайную составляющие. Ее фиксированная составляющая –
, имеет как фиксированную, так и чисто случайную составляющие. Ее фиксированная составляющая – 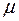 , то есть математическое ожидание
, то есть математическое ожидание 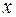 , а ее случайная составляющая –
, а ее случайная составляющая – 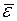 , то есть среднее значение чисто случайной составляющей в выборке.
, то есть среднее значение чисто случайной составляющей в выборке.
Функции плотности вероятности для 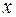 и
и 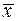 показаны на одинаковых графиках (рис. A.6). Как показано на рисунке, величина
показаны на одинаковых графиках (рис. A.6). Как показано на рисунке, величина 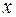 считается нормально распределенной. Можно видеть, что распределения, как
считается нормально распределенной. Можно видеть, что распределения, как 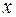 , так и
, так и 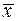 , симметричны относительно
, симметричны относительно 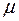 – теоретического среднего. Разница между ними в том, что распределение
– теоретического среднего. Разница между ними в том, что распределение 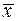 уже и выше. Величина
уже и выше. Величина 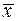 , вероятно, должна быть ближе к
, вероятно, должна быть ближе к 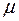 , чем значение единичного наблюдения
, чем значение единичного наблюдения 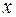 , поскольку ее случайная составляющая
, поскольку ее случайная составляющая 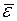 есть среднее от чисто случайных составляющих
есть среднее от чисто случайных составляющих 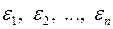 в выборке, которые, по-видимому, «гасят» друг друга при расчете среднего. Далее теоретическая дисперсия величины
в выборке, которые, по-видимому, «гасят» друг друга при расчете среднего. Далее теоретическая дисперсия величины 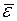 составляет лишь часть теоретической дисперсии
составляет лишь часть теоретической дисперсии 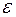 .
.
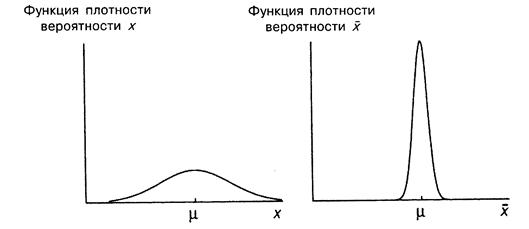
Рис. A.6.
Величина 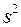 – оценка теоретической дисперсии
– оценка теоретической дисперсии 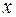 – также является случайной переменной. Вычитая (A.18) из (A.17), имеем:
– также является случайной переменной. Вычитая (A.18) из (A.17), имеем:
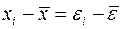 .
.
Следовательно,
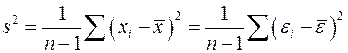 .
.
Таким образом, 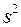 зависит от (и только от) чисто случайной составляющей наблюдений
зависит от (и только от) чисто случайной составляющей наблюдений 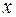 в выборке. Поскольку эти составляющие меняются от выборки к выборке, также от выборки к выборке меняется и величина оценки
в выборке. Поскольку эти составляющие меняются от выборки к выборке, также от выборки к выборке меняется и величина оценки 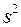 .
.

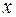 в выборке случайно, поскольку
в выборке случайно, поскольку 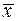 – оценку математического ожидания:
– оценку математического ожидания: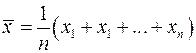 .
. -м наблюдении может быть разложена на две составляющие: постоянную часть
-м наблюдении может быть разложена на две составляющие: постоянную часть 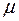 и чисто случайную составляющую
и чисто случайную составляющую 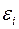 :
: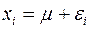 . (A.17)
. (A.17)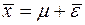 , (A.18)
, (A.18)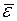 – выборочное среднее величин
– выборочное среднее величин 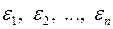 в выборке, которые, по-видимому, «гасят» друг друга при расчете среднего. Далее теоретическая дисперсия величины
в выборке, которые, по-видимому, «гасят» друг друга при расчете среднего. Далее теоретическая дисперсия величины 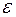 .
.
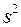 – оценка теоретической дисперсии
– оценка теоретической дисперсии 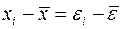 .
.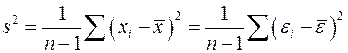 .
.


