Тема 1.2. Корни, степени и логарифмы. Задание 5. Решение линейных, квадратных, рациональных уравнений
Задание 5. Решение линейных, квадратных, рациональных уравнений. – 2 ч. Цель: формирование умения решать линейные, квадратные, рациональные уравнения. Задание для самостоятельной внеаудиторной работы: & 5.1.Вспомните, что называют уравнением? Дайте определения корня уравнения. Что означает фраза «решить уравнение»? Какие уравнения называют линейными, квадратными, рациональными? Какова техника их решения? Основные сведения из теории: 5.2. Закончите определения: 1) Уравнение - …, содержащее … 2) Корень уравнения - …, при подстановке которого уравнение обращается в … 3) Решить уравнение – значит найти все его … или доказать, что … 5.3. Заполните пропуски: · Уравнение вида ах + в = 0, где а, в – заданные числа, · Метод решения линейных уравнений заключается в том, что … · Уравнение вида ах2 + вх+ с = 0 где а, в, с – заданные числа, · Квадратные уравнения бывают полными и … · Корни полного квадратного уравнения находим через дискриминант, где D = …, по формуле · Квадратное уравнение имеет два корня, если D = … · Квадратное уравнение не имеет корней на множестве R, если D = … · Полное квадратное уравнение имеет два равных корня, если D = … · Метод решения неполного квадратного уравнения ах2 + вх = 0 заключается в том, что … · Метод решения неполного квадратного уравнения ах2 + с = 0 заключается в том, что … · Уравнение вида х2 + рх + q = 0 называется… · Для решения приведённых квадратных уравнений можно использовать теорему … · Теорема, обратная теореме Виета: Если числа · Если … — рациональное выражение, то уравнение вида … называют рациональным. · Метод решения рациональных уравнений заключается в том, что … Примеры и упражнения: ? 5.4. Решите уравнения, сводящиеся к линейным: а) ? 5.5. Решите квадратные уравнения: а) C5.6. Пусть х 1 и х 2 - корни квадратного уравнения. Используя теорему, обратную теореме Виета, заполните таблицу по образцу с учётом того, что х 1< х 2.
После решения уравнений точки с полученными координатами нанесите на координатную плоскость и последовательно их соедините. При правильном выполнении вы получите рисунок. ? 5.7. Зная, что х 1 и х 2 - корни квадратного уравнения, применяя теорему Виета, составьте квадратные уравнения по образцу:
? 5.8. Решите дробно-рациональные уравнения: а) ¶ 5.9. При каких k уравнение i5.10.Пройдите тесты на умение решать уравнения: · http: //grustlivaya.edusite.ru/p114aa1.html (линейные уравнения) · http: //www.ankolpakov.ru/testy-po-matematike-dlya-8-klassa-algebra-reshenie-kvadratnyx-uravnenij/ (квадратные уравнения); · http: //reshuege.ru/test? theme=14& ttest=true (линейные и квадратные уравнения); · http: //reshuege.ru/test? theme=9& ttest=true (рациональные уравнения); · http: //321start.ru/demo/demo.php (линейные, квадратные, дробно-рациональные уравнения). Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §5, п. 1, 2, стр. 39 – 42; глава 1, §8, п. 1 - 6, стр. 68 – 75.
|

 ; х – переменная, называется…
; х – переменная, называется… …
… и
и  таковы, что их сумма равна …, а произведение равно …, то эти числа являются корнями уравнения …
таковы, что их сумма равна …, а произведение равно …, то эти числа являются корнями уравнения … ; б)
; б)  ; в)
; в) 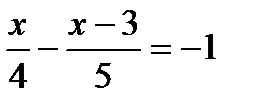 .
. ; б)
; б)  ; в)
; в)  .
.
 ; б)
; б)  .
.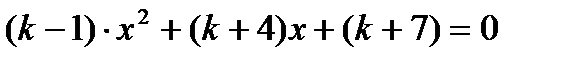 имеет ровно 1 корень?
имеет ровно 1 корень?


