Тема 1.2. Корни, степени и логарифмы
Задание 12. Итоговое повторение по теме 1.2. – 1 ч. Цель: формирование умения проводить преобразования выражений, включающих степени, радикалы, логарифмы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; решать иррациональные, показательные, логарифмические уравнения. Задание для самостоятельной внеаудиторной работы: & 12.1.Вспомните основные свойства степени и логарифма, основные виды уравнений и методы их решений. Основные сведения из теории: 12.2. Для успешного прохождения теста вспомните основные понятия и формулы, изученные в теме «Корни, степени и логарифмы». Заполните пропуски: №1. №2. Корнем n–й степени из числа а ( №3. №4. Метод решения иррациональных уравнений – возведение … Обязательными этапами решения являются запись … и выполнение … №5.Один из методов решения показательных уравнений - приведение обеих частей уравнения к … Если в показательном уравнении основания степени равны, то и показатели степени … №6. №7. Логарифмом числа b по основанию а называют такой …, что … №8. Логарифм числа b по основанию … называют десятичным логарифмом числа b и обозначают … Логарифм числа b по основанию … называют натуральным логарифмом числа b и обозначают … №9. №10. №11. Один из методов решения логарифмических уравнений является использование определения логарифма числа b по основанию а. При решении логарифмических уравнений необходимо выписать … и сделать … решения. №12. Примеры и упражнения: ? 12.3. Пройдите тест (в случае возникновения трудностей, обратитесь к теории из №12.2): Электронная версия теста «Тест 12» находится на прилагаемом к пособию диске. Выберите один правильный ответ: 1. РЕЗУЛЬТАТОМ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЯ А. Б. В. Г. 2. ЗНАЧЕНИЕ ВЫРАЖЕНИЯ А. 0, 3 Б. 0, 9 В. 0, 0003 Г. 0, 0081 3. РЕЗУЛЬТАТ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЯ А. s Б. В. Г. 4. ЕСЛИ А. -7 Б. -19 В. 5 Г. 13 5. ЕСЛИ А. 6 Б. -4 В. -6 Г. -8 6. РЕЗУЛЬТАТ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЯ А. 3 Б. 2 В. 8 Г. 0 7. ЗНАЧЕНИЕ ВЫРАЖЕНИЯ А. 45 Б. -1 В. 0 Г. 3 8. ЗНАЧЕНИЕ ВЫРАЖЕНИЯ А. 300 Б. 9 В. 11 Г. 3002 9. ЗНАЧЕНИЕ ВЫРАЖЕНИЯ А. 2 Б. В. Г. 10. ЗНАЧЕНИЕ ВЫРАЖЕНИЯ А. Б. В. 7 Г. 3 11. СУММА КОРНЕЙ ЛОГАРИФМИЧЕСКОГО УРАВНЕНИЯ А. 16 Б. 0 В. 6 Г. -6 12. ЗНАЧЕНИЕ ВЫРАЖЕНИЯ А. 35 Б. 34 - е В. 34 Г. 33 Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 2, §16-18, 20, п. 1, стр. 110 – 117, 119 – 121, 123 - 124.
|

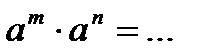 ;
;  ;
; 
 ) называют такое число, … степень которого равна …
) называют такое число, … степень которого равна …  …
… ,
, 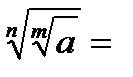 …
…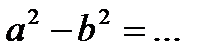
 ;
;  ;
;  ;
; 
 - основное логарифмическое тождество.
- основное логарифмическое тождество. ;
;  .
. ЯВЛЯЕТСЯ
ЯВЛЯЕТСЯ



 РАВНО
РАВНО ИМЕЕТ ВИД
ИМЕЕТ ВИД

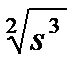
 – КОРЕНЬ УРАВНЕНИЯ
– КОРЕНЬ УРАВНЕНИЯ  , ТО ЗНАЧЕНИЕ ВЫРАЖЕНИЯ
, ТО ЗНАЧЕНИЕ ВЫРАЖЕНИЯ  РАВНО
РАВНО , ТО ЗНАЧЕНИЕ ВЫРАЖЕНИЯ
, ТО ЗНАЧЕНИЕ ВЫРАЖЕНИЯ  РАВНО
РАВНО ИМЕЕТ ВИД
ИМЕЕТ ВИД РАВНО
РАВНО РАВНО
РАВНО РАВНО
РАВНО


 РАВНО
РАВНО

 РАВНА
РАВНА РАВНО
РАВНО


