Тема 1.3. Основы тригонометрии. Задание 15. Решение задач на использование основных тригонометрических тождеств
Задание 15. Решение задач на использование основных тригонометрических тождеств. – 1 ч. Цель: формирование умения использовать основные тригонометрические тождества для преобразования и вычисления значений тригонометрических выражений, доказательства тождеств. Задание для самостоятельной внеаудиторной работы: & 15.1.Внимательно изучите формулы – соотношения между тригонометрическими функциями одного аргумента. Какое тождество называют основным тригонометрическим? Запишите его формулой. Какие приёмы доказательства тригонометрических тождеств Вам известны? Основные сведения из теории: 15.2. Замените символ * так, чтобы выражение стало соотношением между тригонометрическими функциями одного аргумента: · · · · · · Примеры и упражнения: C15.3. Начало учения о тригонометрических величинах было положено в Индии в 4 – 5 веках нашей эры. Индийские учёные впервые в науке стали употреблять линию синуса как половину хорды и составили первые тригонометрические таблицы синусов (полухорд). Им было известно и основное тригонометрическое тождество. Термины «синус» и «косинус» также пришли к нам от индийцев. Установите правильную последовательность косточек математического домино, и Вы узнаете, какому слову на санскрите обязан своим происхождением термин «синус» (в переводе – «половина тетивы лука»):
? 15.4. Упростите тригонометрическое выражение: а) д) ¶з) ? 15.5. Докажите тождество: а) в) ¶15.6. Вычислите: а) Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. – Глава 3, §27, стр. 144 – 146.
|

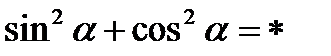 ;
; ;
; ;
;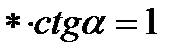 ;
; ;
;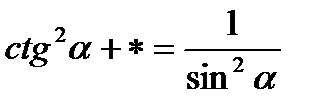 .
.














 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  ; ж)
; ж)  ;
; ; ¶и)
; ¶и)  .
. ; б)
; б)  ;
; ; ¶г)
; ¶г) 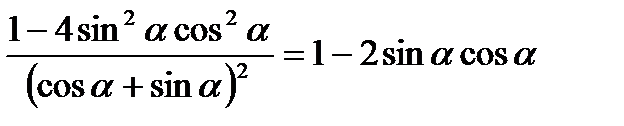 .
. , если
, если  ; б)
; б) 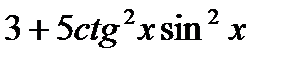 , если
, если  ; в)
; в)  , если
, если  .
.


