ПРАВИЛО ПРИМЕНЕНИЯ ФОРМУЛЫ ПРИВЕДЕНИЯ
1 – выяснить, меняется ли исходная тригонометрическая функция на кофункцию 2 – определить знак исходной тригонометрической функции 3 – привести формулу в стандартный вид 4 – определить четверть, в которой находится аргумент тригонометрической функции 17.4. Установите соответствие:
Примеры и упражнения: Вам, уважаемый студент, известно, что впервые тригонометрию как науку о тригонометрических функциях стал рассматривать знаменитый швейцарский учёный Леонард v До Эйлера тригонометрические функции рассматривались в математике в виде таблиц. Он ввёл определение тригонометрических функций. v Эйлер впервые стал рассматривать тригонометрические функции углов, превышающих v Он вывел формулы приведения. v Эйлер впервые стал систематически излагать тригонометрию аналитическим путём: получал и доказывал теоремы, исходя из небольшого числа основных соотношений.
Выполнив задание C17.5. и заменив получившиеся ответы словами из таблицы, Вы узнаете название этого научного труда. C17.5. Вычислите значение тригонометрического выражения, используя формулы приведения: а) Название научного труда Эйлера:
Карта ответов:
Выполнив задание C17.6. и воспользовавшись картой ответов, Вы узнаете год издания этого научного труда, имеющего колоссальное значение для тригонометрии. C17.6. Вычислите значение тригонометрического выражения: а) Карта ответов:
Как давно это было… А тригонометрию в школе до сих пор без малейших изменений изучают по Эйлеру! Вклад Эйлера в развитие математики огромен. Его работы оказали значительное влияние на развитие математического анализа, теории чисел, приближённых вычислений, дифференциальной геометрии. Прав был один из учителей юного Леонарда, много позже написавший своему знаменитому ученику: «Я посвятил себя детству высшей математики. Ты, мой друг, продолжишь её становление в зрелости». Выполнив задание C17.7. и воспользовавшись картой ответов, Вы узнаете имя и фамилию великого учёного - учителя Эйлера. C17.7. Упростите тригонометрическое выражение: а) Карта ответов:
Гений Эйлера многогранен. Учёного интересовала механика, астрономия, оптика, музыка. Так, его «Письма о разных физических и философских материях, написанные к некоторой немецкой принцессе…» приобрели огромную популярность в 18 -19 веках и выдержали свыше 40 изданий на 10 языках. Гений Эйлера намного опережал время. В 1757 году учёный впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Но в те годы формулы не могли найти практического применения.
Много лет спустя, когда во многих странах стали строить железные дороги, потребовалось рассчитать прочность железнодорожных мостов. Вот тогда модель Эйлера и принесла практическую пользу в проведении экспериментов. Выполнив задание ¶C17.8. и воспользовавшись картой ответов, Вы узнаете, на сколько лет Эйлер опередил своё время формулами для определения критической нагрузки при сжатии упругого стержня.
¶C17.8. Найдите значение тригонометрического выражения: а) в) Карта ответов:
i17.9.Пройдите тесты на применение формул приведения: · http: //reshuege.ru/test? theme=64. · электронная версия теста «Тест 17» находится на прилагаемом к пособию диске. Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §30, стр. 151 – 156.
|









 .
.
 Перед Вами – страницы научного труда Эйлера с изложением его тригонометрических нововведений.
Перед Вами – страницы научного труда Эйлера с изложением его тригонометрических нововведений. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.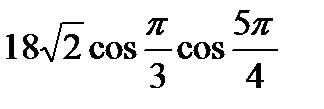 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б) 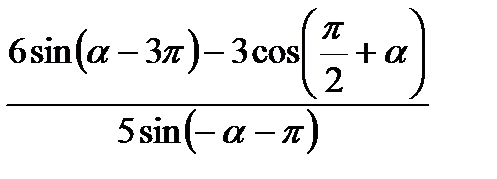 .
.




 , если
, если  ; б)
; б)  , если
, если  и
и  ;
; , если
, если 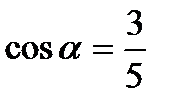 и
и  .
.


