Тема 1.3. Основы тригонометрии. Задание 21. Решение задач на использование формул преобразования сумм тригонометрических функций в произведения и произведений в суммы
Задание 21. Решение задач на использование формул преобразования сумм тригонометрических функций в произведения и произведений в суммы. – 1 ч. Цель: формирование умения использовать формулы преобразования сумм тригонометрических функций в произведения и произведений в суммы для преобразования и вычисления значений тригонометрических выражений. Задание для самостоятельной внеаудиторной работы: & 21.1.Вспомните, какие формулы называют формулами преобразования сумм тригонометрических функций в произведения и произведений в суммы. Запишите эти формулы. Внимательно изучите по учебнику простейшие примеры применения данных формул. Основные сведения из теории: 21.2. Замените символ * так, чтобы выражение стало формулой преобразования суммы (разности) тригонометрических функций в произведение: · · · 21.3. Замените символ * так, чтобы выражение стало формулой преобразования произведений тригонометрических функций в сумму (разность): · · Примеры и упражнения: ? 21.4. Представьте выражение в виде произведения: а) ? 21.5. Представьте выражение в виде произведения: а) ? 21.6. Представьте выражение в виде произведения: а) ? 21.7. Представьте выражение в виде частного: а) ? 21.8. Преобразуйте произведение тригонометрических функций в сумму (разность): а) ? 21.9. Упростите выражение, применяя формулы преобразования сумм тригонометрических функций в произведения и произведений в суммы: а) ¶г) Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §35-36, стр. 165 – 171.
|

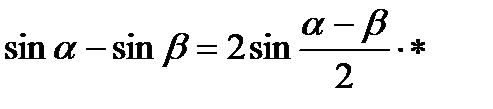 ;
; ;
; .
. ;
; .
.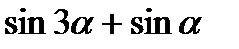 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б) 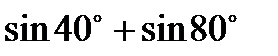 ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  .
.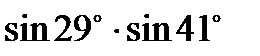 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.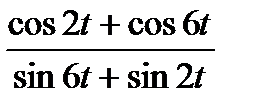 ; б)
; б)  ; в)
; в)  ;
; ; ¶д)
; ¶д)  ; ¶е)
; ¶е)  .
.


