Тема 1.3. Основы тригонометрии. Задание 24. Решение простейших тригонометрических уравнений
Задание 24. Решение простейших тригонометрических уравнений. – 2 ч. Цель: формирование умения вычислять значения обратных тригонометрических функций, решать простейшие тригонометрические уравнения. Задание для самостоятельной внеаудиторной работы: & 24.1.Вспомните определения арксинуса, арккосинуса, арктангенса и арккотангенса действительного числа. Как найти значение обратной тригонометрической функции? Какие формулы позволяют вычислять арксинус, арккосинус, арктангенс и арккотангенс от отрицательного числа? Запишите их. & 24.2.Вспомните, какие уравнения называются простейшими тригонометрическими. Какова техника решения этих уравнений? Внимательно изучите по учебнику примеры решения простейших тригонометрических уравнений. Основные сведения из теории: 24.3. Закончите определение: Арксинусом действительного числа a из отрезка Арккотангенсом действительного числа a называется угол Простейшим тригонометрическим уравнением называется уравнение вида… 24.4.Запишите правую часть формулы, позволяющей находить значение обратной тригонометрической функции от отрицательного аргумента: · · 24.5. Установите соответствие:
24.6. Проанализируйте, какие из следующих утверждений являются верными: Уравнение Уравнение Уравнение Уравнение Примеры и упражнения: C24.7. Широко известная латинская формула утверждает «Scientia vinces». Первое слово в переводе на русский – наукой. Установите правильную последовательность косточек математического домино, и Вы узнаете, перевод второго слова и откроете для себя смысл этой формулы.
? 24.8. Вычислите: а) г) ¶24.9. Вычислите, на сколько процентов число ? 24.10. Решите простейшее тригонометрическое уравнение: а) ж) ? 24.11. Решите простейшее тригонометрическое уравнение: а) е) ? 24.12. Решите простейшее тригонометрическое уравнение. Укажите корни, принадлежащие заданному отрезку: а) ¶24.13. Решите простейшее тригонометрическое уравнение. Укажите его наибольший отрицательный корень: а) i24.14.Пройдите тесты на вычисление значений обратных тригонометрических функций и на решение простейших тригонометрических уравнений: · http: //reshuege.ru/test? theme=13. Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §38-40, стр. 178 – 187.
|

 называется угол
называется угол 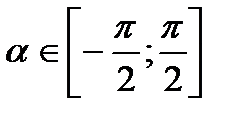 …
… …
…




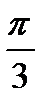
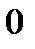



 имеет бесконечное множество решений, представленных серией:
имеет бесконечное множество решений, представленных серией:  Z.
Z.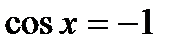 имеет бесконечное множество решений, представленных серией:
имеет бесконечное множество решений, представленных серией:  Z.
Z. имеет бесконечное множество решений, представленных серией:
имеет бесконечное множество решений, представленных серией: 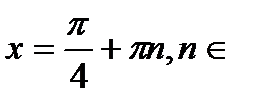 Z.
Z. корней не имеет.
корней не имеет.
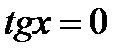
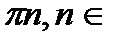 Z
Z
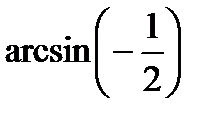


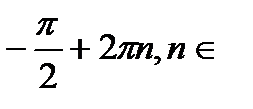 Z
Z




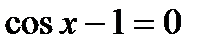
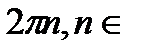 Z
Z
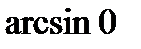
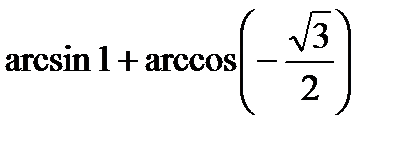 ; б)
; б)  ; в)
; в) 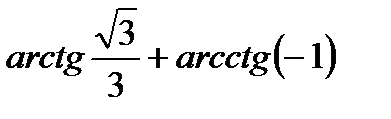 ;
; ; ¶д)
; ¶д) 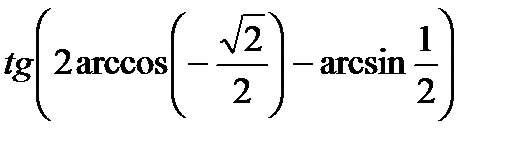 .
. больше числа
больше числа  .
. ; б)
; б) 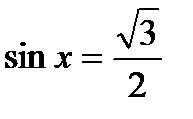 ; в)
; в)  ; г)
; г) 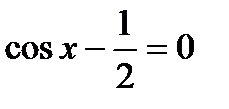 ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и)  ; к)
; к)  ; л)
; л)  ; м)
; м) 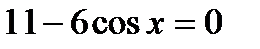 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ;
; ; ¶ж)
; ¶ж)  ; ¶з)
; ¶з)  .
. ,
,  ; б)
; б)  ,
, 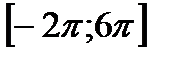 .
.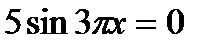 ; б)
; б) 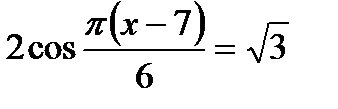 .
.


