Тема 1.3. Основы тригонометрии. Задание 25. Решение тригонометрических уравнений
Задание 25. Решение тригонометрических уравнений. – 1 ч. Цель: формирование умения решать тригонометрические уравнения. Задание для самостоятельной внеаудиторной работы: & 25.1.Вспомните, какие уравнения называются тригонометрическими. Какие методы решения данных уравнений Вам известны? Внимательно изучите по учебнику примеры решения тригонометрических уравнений. Основные сведения из теории: 25.2. Закончите определение: Тригонометрическим уравнением называется уравнение, содержащее переменную… 25.3. Заполните пропуски так, чтобы утверждение стало верным: Из тригонометрических уравнений Из тригонометрических уравнений Примеры и упражнения: ? 25.4. Решите тригонометрическое уравнение, сводящееся к квадратному: а) ? 25.5. Решите тригонометрическое уравнение методом вынесения за скобки общего множителя: а) ? 25.6. Решите тригонометрическое уравнение, применяя формулы тригонометрии: а) г) ? 25.7. Решите однородное тригонометрическое уравнение: а) ¶г) ¶25.8. Решите тригонометрическое уравнение: а) г) д) Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §40, стр. 187 – 190.
|

 ,
,  и
и  третьим лишним является …, так как метод его решения - … отличается от метода решения- … двух других уравнений.
третьим лишним является …, так как метод его решения - … отличается от метода решения- … двух других уравнений. и
и  третьим лишним является …, так как метод его решения - … отличается от метода решения- … двух других уравнений.
третьим лишним является …, так как метод его решения - … отличается от метода решения- … двух других уравнений. ; б)
; б)  ; в)
; в)  ; г)
; г)  , укажите корни уравнения, принадлежащие отрезку
, укажите корни уравнения, принадлежащие отрезку  .
. ; б)
; б)  ; в)
; в) 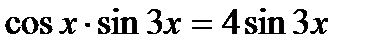 , укажите корни уравнения, принадлежащие отрезку
, укажите корни уравнения, принадлежащие отрезку  .
. ; б)
; б) 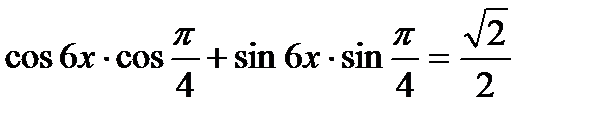 ; в)
; в) 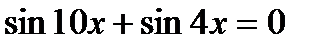 ;
; ; д)
; д) 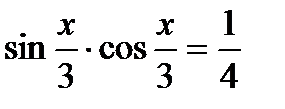 ; е)
; е)  , укажите корни уравнения, принадлежащие отрезку
, укажите корни уравнения, принадлежащие отрезку  .
. ; б)
; б)  ; в)
; в)  ;
; , укажите корни уравнения, принадлежащие отрезку
, укажите корни уравнения, принадлежащие отрезку  .
. ; б)
; б) 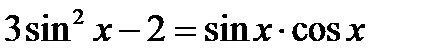 ; в)
; в)  ;
; , укажите корни уравнения, принадлежащие отрезку
, укажите корни уравнения, принадлежащие отрезку  ;
; , найдите наименьший положительный корень уравнения.
, найдите наименьший положительный корень уравнения.


