Тема 1.3. Основы тригонометрии. Задание 27. Итоговое повторение по теме 1.3
Задание 27. Итоговое повторение по теме 1.3. – 1 ч. Цель: формирование умения решать тригонометрические уравнения и неравенства. Задание для самостоятельной внеаудиторной работы: & 27.1.Вспомните основные виды и методы решения тригонометрических уравнений. Как решаются простейшие тригонометрические неравенства? Основные сведения из теории: 27.2. Закончите определение: Тригонометрическим уравнением называется… Простейшим тригонометрическим неравенством называется… 27.3. Установите соответствие:
Академик Алексей Николаевич Крылов (1863-1945) – выдающийся русский кораблестроитель, механик и математик. Работы А.Н. Крылова по теории кораблестроения ещё в начале двадцатого столетия принесли ему мировую известность. Сфера интересов академика была многогранной. Это теория и практика отечественного кораблестроения; проектирование и строительство современных военно-морских кораблей; подготовка высококвалифицированных кадров для военно-морского флота и, конечно, математика. Непревзойдённый её знаток, академик Крылов вдохновлялся математикой в своих работах. Это вдохновение Алексей Николаевич всегда использовал для эффективного решения конкретных научно – технических проблем и делал это так, что после него ничего добавить было нельзя. Выполнив задания C27.4. - 27.5. и заменив получившиеся ответы словами из таблицы, Вы откроете для себя замечательную цитату академика А.Н. Крылова. C27.4. Решите тригонометрическое уравнение: а) г) ж) ¶к) C27.5. Решите тригонометрическое уравнение: а) б) ¶в) Цитата А.Н.Крылова:
Карта ответов:
? 27.6. Решите простейшее тригонометрическое неравенство: а) i27.7.Пройдите тесты на преобразование тригонометрических выражений, решение тригонометрических уравнений и простейших тригонометрических неравенств: http: //le-savchen.ucoz.ru/publ/12-1-0-65%20. Список литературы: 1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.-395 с. - Глава 3, §39-41, стр. 181 – 193.
|







 Примеры и упражнения:
Примеры и упражнения: ; б)
; б)  ; в)
; в) 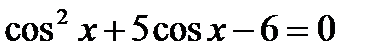 ;
; ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и)  ;
; .
. , в ответе укажите корни уравнения, принадлежащие отрезку
, в ответе укажите корни уравнения, принадлежащие отрезку 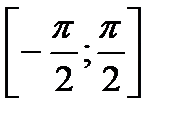 ;
; , в ответе укажите наименьший положительный корень уравнения;
, в ответе укажите наименьший положительный корень уравнения;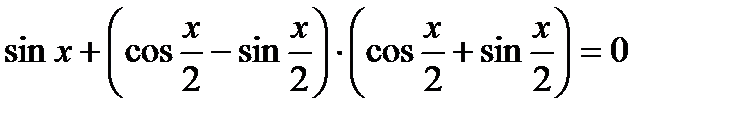 , в ответе укажите корни уравнения, принадлежащие отрезку
, в ответе укажите корни уравнения, принадлежащие отрезку  .
. Z;
Z;
 Z
Z
 Z
Z
 Z;
Z;
 Z
Z
 Z
Z
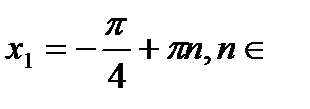 Z;
Z;
 Z
Z
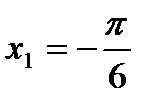 ;
;

 Z;
Z;
 Z
Z
 Z
Z
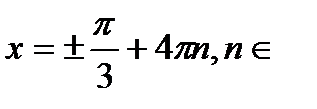 Z
Z
 Z;
Z;
 Z
Z
 ;
;

 Z
Z
 Z
Z
 Z;
Z;
 Z
Z
 Z
Z
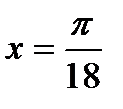
 Z
Z
 Z
Z

 Z;
Z;
 Z
Z
 ,
,

 Z
Z
 Z
Z

 ; б)
; б)  .
.


