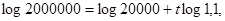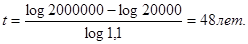Примеры решения задач. Задача 1.Допустим, рыночная ставка заработной платы на рынке определенного вида труда установилась на уровне 35 руб
Задача 1. Допустим, рыночная ставка заработной платы на рынке определенного вида труда установилась на уровне 35 руб. в час. Предложение труда (тысячи человеко-часов) описывается уравнением: L = 2W – 60. а) определите объем экономической ренты;
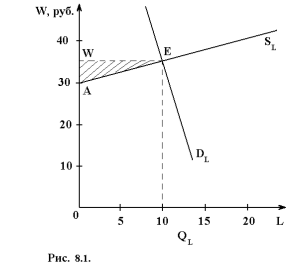
б) постройте график и обозначьте площадь, соответствующую объему ренты, и площадь, соответствующую альтернативным издержкам труда, за которые работники согласны предлагать свой труд на данном рынке. Решение. а) Подставим в уравнение L = 2W – 60 значение ставки заработной платы – 35 руб. Тогда объем использования труда составит 10 единиц. Если L = 2W – 60, то W = 30 + 0, 5L. При L = 0, W = 30. Тогда сумма экономической ренты 0, 5*10*(35 – 30) = 25 000 руб. б) См. рис. 8.1. Площадь треугольника AWE представляет экономическую ренту, а площадь, равная 0AEQ удержать работников от ухода с данного рынка. Задача 2. На основании данных таблицы 8.1 рассчитайте предельную чистую окупаемость инвестиций двух конструкций, предлагаемых рынком, и определите, какая из них окажется предпочтительнее для предприятия при ставке ссудного процента r = 45% и какова при этом будет предельная чистая прибыль. Предлагаемая цена реализации единицы продукции – 600 ден. ед. Таблица 8.1
Решение. Для определения наиболее предпочтительной конструкции предприятию необходимо рассчитать и сопоставить предельную чистую окупаемость предлагаемых конструкций, которая равна: MRR 1) определим предельную доходность инвестиций: MRP 2) расчет предельного чистого дохода инвестиций: R = MRP 3) предельная норма окупаемости инвестиций определяется по формуле: MRR 4) предельная чистая окупаемость конструкции 1 отрицательна –2, 5% (42, 5 – 45), а второй – положительна 1, 67 % (46, 67 – 45). Предпочтительнее для предприятия 2-я конструкция; 5) предельная прибыль от использования конструкции 1 составит –100 ден. ед. [1700 – (4000*0, 45)], а второй = 100 ден. ед. [2800 – (6000*0, 45)]. Решение задачи представлено в таблице 8. 2: Таблица 8.2
Задача 3. Спрос на землю описывается уравнением Q = 150 – 2R, где Q – площадь используемой земли, R – рента (в млн. руб. за 1 га). а) Какова будет равновесная ставка земельной ренты, если площадь доступных земельных угодий составляет 95 га? б) Какова будет цена 1 га земли, если ставка банковского процента составит 55 %. Решение. а) Равновесный уровень ренты определим решив уравнение: 150 – 2R = 95, откуда рента равна 27, 5 млн. руб. за 1 га земли. б) Цена земли – это текущая дисконтированная стоимость земельной ренты, следовательно, цена 1 га земли равна 27, 5/0, 55 = 50 млн. руб.
Задача 4. Коммерческая фирма положила 20 тыс. д.е. на срочный вклад при процентной ставке 10 % годовых (с учетом процентов на проценты). Через несколько лет вклад превратился в 2 млн. д.е. Через какое время это произойдет (при прочих равных условиях)? Решение. Величина выплаты по вкладу (с учетом процентов на проценты) К рассчитывается по формуле сложных процентов:
где В – величина вклада, n – процентная ставка, t – срок вклада. Подставляя значения получим:
Логарифмируем:
откуда:
Основные понятия и их определения.
|

 – сумму заработной платы, необходимую для того, чтобы
– сумму заработной платы, необходимую для того, чтобы – r. Ее расчет может быть осуществлен в следующей последовательности:
– r. Ее расчет может быть осуществлен в следующей последовательности: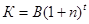 ,
,