Корневые методы
Как было рассмотрено в разд. 5, вид корней характеристического уравнения Для оценки быстродействия системы используется понятие «степени устойчивости».Термин «степень устойчивости» не является удачным, и его следовало бы заменить термином «степень быстродействия». Это объясняется тем, что «степень устойчивости» никак не связана с удалением системы от границы устойчивости, определяемым по склонности системы к колебаниям, но этот термин используется в специальной литературе по ТАУ. Под степенью устойчивости h понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 7.6).
Рис. 7.6. Степень устойчивости
Могут быть два случая: когда ближайший корень является вещественным (рис. 7.6, а) и когда к оси мнимых ближе всего расположена пара комплексных корней (рис. 7.6, б). Корни характеристического уравнения, расположенные ближе всего к оси мнимых, то есть имеющие наименьшую по абсолютной величине вещественную часть, дают в переходном процессе слагаемые (5.8)
которые затухают наиболее медленно. В большинстве случаев переходный процесс можно считать закончившимся тогда, когда затухнет слагаемое, определяемое ближайшим к мнимой оси корнем. Если ближайшим к мнимой оси является вещественный корень, то составляющая в переходном процессе, от этого корня, будет иметь вид
Допустив в конце переходного процесса
Так, например, если принять Δ = 0, 05, то время переходного процесса составит
Если ближайшей к мнимой оси является пара комплексных корней
В этом случае, допустив
Таким образом, и в этом случае величина степени устойчивости будет определять быстроту затухания переходного процесса. Важным обстоятельством является то, что степень устойчивости можно найти без вычисления значений корней характеристического уравнения. Для этой цели в характеристическом уравнении (5.6) переходят к новой переменной z = d + h. Подставляя в него d = z – h, получаем так называемое смещенное уравнение
Раскрывая скобки в (7.31) и группируя подобные члены, имеем:
Это уравнение соответствует смещению осей на плоскости корней (см. рис. 7.6) влево на величину h. В результате один (см. рис. 7.6, а) или два (см. рис. 7.6, б) корня попадают на ось мнимых, что соответствует границе устойчивости. Для вычисления степени устойчивости необходимо применить к смещенному характеристическому уравнению (7.32) любой критерий устойчивости и определить при каком значении h получается граница устойчивости. Напомним, что апериодической границе устойчивости соответствует равенство нулю свободного члена характеристического уравнения
а колебательной границе устойчивости соответствует равенство нулю предпоследнего определителя Гурвица, прохождение кривой Михайлова через начало координат. Обратимся теперь к оценке запаса устойчивости системы автоматического регулирования. Склонность системы к колебаниям наблюдается, если в решении характеристического уравнения будут присутствовать комплексные корни вида
Колебательность связана с другим корневым показателем запаса устойчивости, так называемым затуханием. Комплексные сопряженные корни дают в выражении для переходного процесса (5.8) слагаемые вида
Найдем затухание амплитуды синусоидального колебания за один период. При некотором значении времени t = t1 эта амплитуда составит
Через один период
Затуханием за период называют величину
Эта величина обычно выражается в процентах. Подставляя значение амплитуды А2 в (7.38), имеем:
или
Обычно в системах автоматического регулирования допускается затухание за один период не менее чем 90 – 98 %. Так например, если h = 98 %, то допустимая колебательность при этом составит
Соответственно при h = 90 % получаем Задание определенной колебательности заставляет ограничивать область расположения корней двумя лучами (рис. 7.7, а), которые составляют с вещественной осью угол
Колебательность системы можно определить без нахождения корней характеристического уравнения подобно тому, как это было рассмотрено выше по отношению к степени устойчивости.
Рис. 7.7. Область расположения корней
При задании допустимых значений колебательности и степени устойчивости область расположения корней должна ограничиваться также вертикальной прямой, проходящей параллельно оси мнимых на расстоянии h (рис. 7.7, б). Расположению корней в этой области соответствует соблюдению требуемого запаса устойчивости, определяемого величиной колебательности m (или затуханием h) и требуемой степенью устойчивости h, характеризующей быстродействие системы. Использование корней характеристического уравнения для оценки качества регулирования является не совсем полным, так как вид переходного процесса определяется не только левой, но и правой частью дифференциального уравнения (4.14) или (4.15). Для того чтобы учесть это обстоятельство, рассмотрим зависимость между регулируемой величиной и управляющим воздействием, записанное посредством передаточной функции замкнутой системы (4.17)
Передаточная функция замкнутой системы представляет собой дробно-рациональную функцию
Раскладывая числитель и знаменатель (7.44) на множители, имеем
Корни числителя b1 – bm называются нулями передаточной функции, так как в точке р = bi передаточная функция обращается в нуль. Корни знаменателя a1 – an являются корнями характеристического уравнения, и они называются полюсами передаточной функции, то есть при р = ai передаточная функция обращается в бесконечность. Полюса передаточной функции характеризуют левую часть дифференциального уравнения, а нули – правую. Задание области расположения полюсов и нулей позволяет более полно оценить вид переходного процесса. Не останавливаясь на подробном анализе, укажем без доказательства общие рекомендации, которых желательно придерживаться при выборе расположения полюсов и нулей передаточных функций. 1. Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от области полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе. 2. Для уменьшения отклонений в переходном процессе часто бывает выгодно удалять полюсы друг от друга. 3. Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси. Кроме этих рекомендаций, сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованиями обеспечения определенного запаса устойчивости и быстродействия (см. рис. 7.7, б). Необходимо отметить, что случай
|

 определяет характер переходных процессов в системе автоматического регулирования. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая сами переходные процессы, а накладывая определенные условия на корни характеристического уравнения.
определяет характер переходных процессов в системе автоматического регулирования. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая сами переходные процессы, а накладывая определенные условия на корни характеристического уравнения.
 , (7.25)
, (7.25)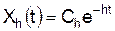 . (7.26)
. (7.26) (где Δ = 0, 01¸ 0, 05 – ошибка регулирования), можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса
(где Δ = 0, 01¸ 0, 05 – ошибка регулирования), можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса . (7.27)
. (7.27) . (7.28)
. (7.28) , то вместо (7.26) будем иметь
, то вместо (7.26) будем иметь .(7.29)
.(7.29) , нельзя в общем виде определить время переходного процесса, так как для этой цели потребовалось бы решить трансцендентное уравнение. Однако можно найти верхнюю границу переходного процесса, положив в этом уравнении
, нельзя в общем виде определить время переходного процесса, так как для этой цели потребовалось бы решить трансцендентное уравнение. Однако можно найти верхнюю границу переходного процесса, положив в этом уравнении 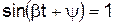 . Тогда имеем:
. Тогда имеем: . (7.30)
. (7.30) . (7.31)
. (7.31) . (7.32)
. (7.32) , (7.33)
, (7.33) . Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью
. Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью . (7.34)
. (7.34) . (7.35)
. (7.35)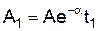 . (7.36)
. (7.36) имеем:
имеем: . (7.37)
. (7.37) . (7.38)
. (7.38) (7.39)
(7.39) . (7.40)
. (7.40) . (7.41)
. (7.41) .
. . (7.42)
. (7.42)
 . (7.43)
. (7.43) . (7.44)
. (7.44) . (7.45)
. (7.45) соответствует отсутствию нулей передаточной функции (7.44). В этом случае вид переходного процесса характеризуется только расположением полюсов.
соответствует отсутствию нулей передаточной функции (7.44). В этом случае вид переходного процесса характеризуется только расположением полюсов.


