Классический метод
Пусть система автоматического регулирования описывается линейным дифференциальным уравнением с правой частью
где р – оператор дифференцирования. Решение этого уравнения можно представить в виде суммы частного и общего решений
Первое слагаемое (6.2) называют вынужденным решением. В случае Хчастн(t) = const это будет установившееся значение, а второе слагаемое – переходная составляющая
Общее решение (переходная составляющая) находится из дифференциального уравнения (6.1) с правой частью, равной нулю
Как уже указывалось выше, это решение определяется выражением (5.8). Полное решение в результате будет иметь вид
где d1 – dn – корни характеристического уравнения
соответствующего дифференциальному уравнению (6.1). Таким образом, для отыскания полного решения дифференциального уравнения (6.1) необходимо найти частное или вынужденное решение уравнения с правой частью ХВ(t) и определить корни характеристического уравнения. Дальнейшим шагом является отыскание произвольных постоянных интегрирования С1 – Сn. Для этой цели используются начальные условия: t = 0; Операции вычисления корней и совместного решения n алгебраических уравнений являются трудоёмкими. Это особенно относится ко второй операции, так как вычисление корней может быть сделано довольно быстро приближенными методами. В связи с этим использование классического метода построения кривой переходного процесса ограничивается случаем сравнительно не высокого порядка дифференциального уравнения.
|

 , (6.1)
, (6.1) . (6.2)
. (6.2) . (6.3)
. (6.3) . (6.4)
. (6.4) , (6.5)
, (6.5) , (6.6)
, (6.6)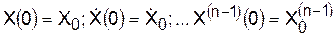 . Начальные условия накладываются на основании физических соображений или находятся из дифференциального уравнения (6.1). Дифференцируя уравнение (6.5) по времени (n – 1) раз и подставляя начальные условия, получают n алгебраических уравнений (исходное уравнение (6.5) и (n – 1) результатов дифференцирования), куда входит n неизвестных – постоянных интегрирования. Совместное решение этих уравнений даёт возможность определить искомые постоянные интегрирования С1 – Сn.
. Начальные условия накладываются на основании физических соображений или находятся из дифференциального уравнения (6.1). Дифференцируя уравнение (6.5) по времени (n – 1) раз и подставляя начальные условия, получают n алгебраических уравнений (исходное уравнение (6.5) и (n – 1) результатов дифференцирования), куда входит n неизвестных – постоянных интегрирования. Совместное решение этих уравнений даёт возможность определить искомые постоянные интегрирования С1 – Сn.


