Критерий устойчивости Михайлова
Рассмотрим отдельно левую часть характеристического уравнения (5.7), которая представляет собой характеристический полином
Подставим в этот полином чисто мнимое значение p = jw, где w представляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического решения. В этом случае получим характеристический комплекс
где вещественная часть будет содержать четные степени частоты
а мнимая – нечетные степени частоты
Практически кривая Михайлова строится по точкам, причем задаются различные значения частоты w и по формулам (5.28), (5.29) вычисляются U(w) и V(w). Результаты расчетов сводятся в табл. 5.1.
Таблица 5.1 Построение кривой Михайлова
По этой таблице строится сама кривая (рис. 5.4). Определим, чему должен равняться угол поворота y вектора D(jw) при изменении частоты w от нуля до бесконечности. Для этого запишем характеристический полином в виде произведения сомножителей
где d1 – dn – корни характеристического уравнения. Характеристический вектор можно тогда представить в следующем виде:
Каждая из скобок представляет собой комплексное число. Следовательно, D(jw) представляет собой произведение n комплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора D(jw) будет равен сумме углов поворота отдельных сомножителей (5.31) при изменении частоты w от нуля до бесконечности
Определим каждое слагаемое в (5.31) по отдельности. Для обобщения задачи рассмотрим различные виды корней. 1. Пусть какой-либо корень, например d1, является вещественным и отрицательным, то есть d1 = –a1. Сомножитель в выражении (5.31), определяемый этим корнем, будет иметь вид (a1 + jw). Построим годограф этого вектора на комплексной плоскости при изменении частоты w от нуля до бесконечности (рис. 5.5, а). При w = 0 вещественная часть U = a1, а мнимая V = 0. Этому соответствует точка А, лежащая на вещественной оси. При w ¹ 0 вектор будет так изменяться, что его вещественная часть будет по-прежнему равна a, а мнимая V = w (точка В на графике). При увеличении частоты до бесконечности вектор уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой, проходящей через точку А, а вектор поворачивается против часовой стрелки.
Рис. 5.5. Вещественные корни Результирующий угол поворота вектора y1 = +(p / 2). 2. Пусть теперь корень d1 является вещественным и положительным, то есть d1 = +a1.Тогда сомножитель в (5.31), определяемый этим корнем будет иметь вид (–a1 + jw). Аналогичные построения (рис. 5.5, б) показывают, что результирующий угол поворота будет y1 = –(p / 2). Знак минус показывает, что вектор поворачивается по часовой стрелке. 3. Пусть два сопряженных корня, например d2 и d3, являются комплексными с отрицательной вещественной частью, то есть При w = 0 начальные положения двух векторов определяются точками А1 и А2 (рис. 5.6, а). Первый вектор повернут относительно вещественной оси по часовой стрелке на угол, равный arctg(b / a), а второй вектор – на тот же угол против часовой стрелки. При постепенном увеличении w от нуля до бесконечности концы обоих векторов уходят вверх в бесконечность и оба вектора в пределе сливаются с мнимой осью. Результирующий угол поворота первого вектора y2 = (p / 2) + g. Результирующий угол поворота второго вектора y3 = (p / 2) – g. Вектор, соответствующий произведению (a – jb + jw)(a + jb + jw) повернется на угол y2 + y3 = 2p / 2 = p.
Рис. 5.6. Комплексные корни
4. Пусть те же комплексные корни имеют положительную вещественную часть, то есть d2; 3 = +a ± jb. Проводя построение аналогично рассмотренному ранее случаю (рис 5.6, б), получим результирующий угол поворота y2 + y3 = –2p / 2 = –p. Таким образом, если характеристическое уравнение будет иметь f корней с положительной вещественной частью, то, каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворотов, равная –f(p / 2). Всем же остальным (n – f) корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворотов, равная +(n – f)(p / 2). В результате общий угол поворота вектора D(jw) при изменении частоты w от нуля до бесконечности по формуле (5.32) будет иметь вид
y = (n – f)(p / 2) – f(p / 2) = n (p / 2) – f p. (5.33)
Этим выражением и определяется искомая связь между формой кривой Михайлова и знаками вещественных частей корней характеристического уравнения. В 1936 г. А.В. Михайловым был сформулирован следующий критерий устойчивости для линейных систем любого порядка. Для устойчивости системы n-го порядка необходимо и достаточно, чтобы вектор D(jw), описывающий кривую Михайлова, при изменении w от нуля до бесконечности имел угол поворота y =n (p / 2). Эта формулировка непосредственно вытекает из (5.33). Для устойчивости системы необходимо, чтобы все корни лежали в левой полуплоскости. Отсюда определяется требуемый результирующий угол поворота вектора. Критерий устойчивости Михайлова формулируется следующим образом: для устойчивости линейной САР необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности, начавшись на положительной полуплоскости и не пересекая начала координат, последовательно пересек столько квадрантов комплексной плоскости, какой порядок имеет полином характеристического уравнения системы.
Для устойчивой системы кривая Михайлова проходит последовательно n квадрантов комплексной плоскости. Наличие границы устойчивости всех трех типов может быть определено по кривой Михайлова следующим образом. При наличии границы устойчивости первого типа (нулевой корень) отсутствует свободный член характеристического полинома an = 0, и кривая Михайлова выходит из начала координат (рис. 5.9, кривая 1)
При границе устойчивости второго типа (колебательная граница устойчивости) левая часть характеристического уравнения, то есть характеристический полином, обращается в нуль при подстановке p = jw0
D(jw0) = X(w0) + Y(w0) = 0. (5.34)
Откуда вытекают два равенства: X(w0) = 0; Y(w0) = 0. Это значит, что точка w = w0 на кривой Михайлова попадает в начало координат (рис. 5.9, кривая 2). При этом величина w0 есть частота незатухающих колебаний системы. Для границы устойчивости третьего типа (бесконечный корень) конец кривой Михайлова перебрасывается (рис. 5.9, кривая 3) из одного квадранта в другой через бесконечность. При этом коэффициент а0 характеристического полинома (5.7) будет проходить через нулевое значение, меняя знак с плюса на минус.
5.4. Определение устойчивости Для определения устойчивости по логарифмическим характеристикам используется критерий устойчивости Найквиста, но строится не амплитудно-фазовая характеристика САР, а логарифмическая амплитудная частотная характеристика и логарифмическая фазовая частотная характеристика разомкнутой системы. Построение ЛАХ выполняется по выражению
L(w) = 20 lg A(w) = 20 lg ½ W(jw)½. (5.35)
В абсолютно устойчивых системах фазовый сдвиг может достигать значения y = –1800 только при модулях, меньших чем единица. В условно устойчивых системах фазовый сдвиг может достигать –1800 чётное число раз (два, четыре и т. д.) (рис. 5.10, в).
Рис. 5.10. Примеры ЛАХ и ЛФХ разомкнутых САР
Это позволяет легко определить устойчивость по виду ЛАХ и ЛФХ разомкнутой системы. На рис. 5.10, а изображен случай абсолютно устойчивой системы. Точка пересечения ЛАХ с осью нуля децибел (точка 1) лежит левее точки, где фазовый сдвиг достигает значения y = –1800 (точка 2). На рис. 5.10, б изображен случай условно устойчивой системы. Точка 1 по-прежнему лежит левее точки 2, но фазовый сдвиг достигает значения y = ‑ 1800 дважды при модулях, больших чем единица (точки 3 и 4). На рис. 5.10, в изображен случай колебательной границы устойчивости и на рис. 5.10, г – случай неустойчивой системы. Контрольные вопросы 1. Сформулируйте понятие устойчивости и неустойчивости линейных систем. 2. Опишите алгебраический критерий устойчивости Гурвица. 3. Опишите критерий устойчивости Михайлова. 4. Назовите границы устойчивости по критерию устойчивости Михайлова. 5. Как определяют устойчивость по ЛАХ и ЛФХ?
6. ПОСТРОЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА Общие положения Переходный процесс в системе автоматического регулирования может вызываться приложением управляющего или возмущающего воздействия, а также вследствие наличия ненулевых начальных условий. Переходный процесс может быть построен либо для регулируемой величины Х(t), либо для ошибки х(t) = Y(t) – X(t). При управляющем воздействии Y(t) = 0 функции переходного процесса отличаются только знаками, так как в этом случае х(t) = – X(t). В дальнейшем изложении будем рассматривать построение кривой переходного процесса только для регулируемой величины. При известном управляющем воздействии легко может быть найдена также и кривая переходного процесса для ошибки. При нахождении кривой переходного процесса в системе автоматического регулирования имеются две сложности. Первая сложность принципиального характера заключается в том, что в реальных системах регулирования управляющие и возмущающие воздействия не являются известными функциями времени, а носят случайный характер. В связи с этим приходится рассматривать некоторые типовые входные воздействия. Типовые входные воздействия стремятся выбирать так, чтобы они были по возможности близкими к реальным воздействиям в системе автоматического регулирования. Три типовых воздействия изображены на рис. 6.1. Воздействие первого типа часто встречается в системах автоматического регулирования в виде внезапного скачка управляющего или возмущающего воздействия на некоторую постоянную величину, например, увеличение напряжения на тяговом двигателе при ступенчатом регулировании, увеличение момента на валу двигателя и т. п. Реакция системы на воздействие этого типа представляет собой ее переходную функцию (рис. 6.1, а). Воздействие второго типа также встречается в системах регулирования в виде кратковременного удара нагрузки, например при коротком замыкании генератора, который отключается через небольшой промежуток времени системой защиты, при кратковременном изменении момента нагрузки двигателя и т. д. Реакция системы на воздействие этого типа представляет ее функцию веса (рис. 6.1, б).
Рис. 6.1. Типовые входные воздействия
Воздействие третьего типа является характерным для следящих систем, когда командная ось внезапно начинает двигаться с некоторой постоянной скоростью. В этом случае исполнительная ось после завершения переходного процесса также будет двигаться с этой скоростью (рис. 6.1, в). Вторая сложность непринципиального характера заключается в том, что обычно системы регулирования описываются дифференциальными уравнениями сравнительно высокого порядка. Это усложняет практические расчеты, поэтому для облегчения задачи построения кривой переходного процесса во многих случаях приходится пользоваться приближенными методами. Для построения кривой переходного процесса часто используют численные и графические методы решения дифференциальных уравнений. Таких методов существует много. Применительно к задачам теории автоматического регулирования удобным оказывается численно-графический метод, разработанный Д.А. Башкировым [6]. Для получения переходных процессов с большим успехом и весьма широко применяются компьютеры. Для сложных автоматических систем в настоящее время этому методу отдается предпочтение. В инженерной практике наиболее распространены способы построения кривой переходного процесса методом непосредственного решения линейных дифференциальных уравнений или так называемый классический метод, использующий преобразования Фурье, Лапласа и Карсона–Хевисайда, а также метод трапецеидальных вещественных частотных характеристик. Рассмотрим в настоящем разделе оба эти метода.
|

 . (5.26)
. (5.26) , (5.27)
, (5.27) , (5.28)
, (5.28) . (5.29)
. (5.29) Если заданы все коэффициенты и определенное значение частоты w, то величина D(jw) изобразится на комплексной плоскости в виде точки с координатами U и V или в виде вектора, соединяющего эту точку с началом координат. Если же значение частоты w менять непрерывно от нуля до бесконечности, то вектор будет изменяться по величине и направлению, описывая своим концом некоторую кривую (годограф), которая называется кривой Михайлова (рис. 5.4).
Если заданы все коэффициенты и определенное значение частоты w, то величина D(jw) изобразится на комплексной плоскости в виде точки с координатами U и V или в виде вектора, соединяющего эту точку с началом координат. Если же значение частоты w менять непрерывно от нуля до бесконечности, то вектор будет изменяться по величине и направлению, описывая своим концом некоторую кривую (годограф), которая называется кривой Михайлова (рис. 5.4). , (5.30)
, (5.30) . (5.31)
. (5.31) . (5.32)
. (5.32)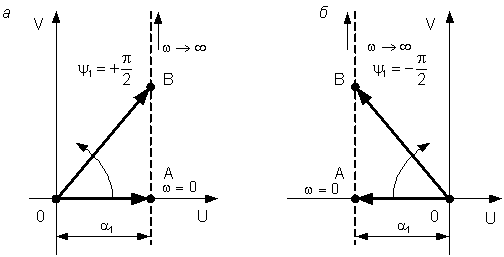

 Оказывается, что кривая Михайлова для устойчивых систем всегда имеет плавную спиральную форму, причем конец ее уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического уравнения (рис. 5.7). Больше чем n число квадрантов кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектора D(jw) оказывается меньше, чем n (p / 2) (рис. 5.8).
Оказывается, что кривая Михайлова для устойчивых систем всегда имеет плавную спиральную форму, причем конец ее уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического уравнения (рис. 5.7). Больше чем n число квадрантов кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектора D(jw) оказывается меньше, чем n (p / 2) (рис. 5.8). Рис. 5.8. Неустойчивая САР
Рис. 5.8. Неустойчивая САР
 Рис. 5.9. Границы устойчивости
Рис. 5.9. Границы устойчивости





