Неустойчивые звенья
Рассмотренные выше звенья позиционного типа относятся к устойчивым звеньям или звеньям с самовыравниванием. Под самовыравниванием понимается способность звена самопроизвольно приходить к новому установившемуся режиму при ограниченном изменении входной величины или возмущающего воздействия. Термин «самовыравнивание» обычно применяется для звеньев, представляющих собой объекты регулирования. Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например звенья интегрирующего типа. Они были рассмотрены выше. Существуют звенья, у которых этот процесс выражен еще заметнее. Это объясняется наличием положительных вещественных корней или комплексных корней с положительной вещественной частью в характеристическом уравнении (в знаменателе передаточной функции, приравненном нулю), в результате чего звено относится к категории неустойчивых звеньев. Рассмотрим в качестве примера звено, описываемое дифференциальным уравнением вида
или
Этому дифференциальному уравнению соответствует передаточная функция
Эта характеристика изображена на рис. 3.33. Таким звеном может быть, например, асинхронный двухфазный управляемый двигатель, если он имеет механическую характеристику с отрицательным наклоном. На рис. 3.34 изображены возможные варианты механических характеристик двигателя для области малых скоростей.
Рис. 3.34. Варианты механических характеристик двигателя для малых скоростей
График на рис. 3.34, а соответствует положительному наклону механических характеристик. В этом случае скорость двигателя связана с управляющим напряжением передаточной функцией, соответствующей устойчивому апериодическому звену первого порядка
где Это звено обладает положительным самовыравниванием или просто самовыравниванием. График на рис. 3.34, б соответствует независимости вращающего момента двигателя от скорости его вращения. В этом случае скорость двигателя связана с управляющим напряжением передаточной функцией, соответствующей интегрирующему звену
где kМ – коэффициент пропорциональности между вращающим моментом и напряжением; J – момент инерции. Это звено не имеет самовыравнивания. График на рис. 3.34, в соответствует механическим характеристикам с отрицательным наклоном, то есть характеристикам неустойчивого типа. В этом случае скорость вращения и напряжение связаны между собой передаточной функцией вида (3.89)
что соответствует отрицательному самовыравниванию. Существенной особенностью неустойчивых звеньев является наличие больших по сравнению с устойчивыми звеньями фазовых сдвигов. Так, для рассмотренного выше апериодического звена с отрицательным самовыравниванием имеем частотную передаточную функцию
Модуль её не отличается от модуля частотной передаточной функции апериодического звена с положительным самовыравниванием (3.33)
а фаза
имеет большое значение по сравнению со вторым уравнением в (3.33). В связи с этим неустойчивые звенья относят к группе так называемых неминимально-фазовых звеньев. К неминимально-фазовым звеньям относятся также устойчивые звенья, имеющие в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительные корни или комплексные корни с положительной вещественной частью. Например, звено с передаточной функцией
относится к группе неминимально-фазовых звеньев. К неустойчивым звеньям относится также ряд других звеньев, имеющих передаточные функции вида
Наличие в автоматической системе неустойчивых звеньев вызывает некоторые особенности расчета.
Контрольные вопросы 1. Дайте понятие типового динамического звена и передаточных функций. 2. Назовите временные характеристики звеньев. 3. Назовите частотные характеристики звеньев. 4. Назовите логарифмические частотные характеристики звеньев. 5. Опишите безинерционное звено и его характеристики. 6. Опишите апериодическое звено первого порядка и его характеристики. 7. Опишите апериодическое звено второго порядка и его характеристики. 8. Опишите идеальное интегрирующее звено и его характеристики. 9. Опишите инерционное интегрирующее звено и его характеристики. 10. Опишите идеальное дифференцирующее звено и его характеристики. 11. Опишите реальное дифференцирующее звено и его характеристики. 12. Опишите неустойчивое звено и его характеристики.
|

 (3.87)
(3.87)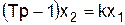 . (3.88)
. (3.88) . (3.89)
. (3.89)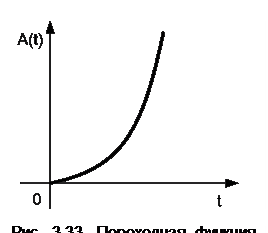 Переходная функция звена представляет собой показательную функцию с положительным показателем
Переходная функция звена представляет собой показательную функцию с положительным показателем . (3.90)
. (3.90)
 , (3.91)
, (3.91) – электромеханическая постоянная времени двигателя; k – коэффициент пропорциональности между установившейся скоростью и напряжением.
– электромеханическая постоянная времени двигателя; k – коэффициент пропорциональности между установившейся скоростью и напряжением. , (3.92)
, (3.92) , (3.93)
, (3.93) . (3.94)
. (3.94) , (3.95)
, (3.95) (3.96)
(3.96) (3.97)
(3.97) ; (3.98)
; (3.98) ; (3.99)
; (3.99) ; (3.100)
; (3.100) . (3.101)
. (3.101)


