Идеальное дифференцирующее звено

Звено описывается уравнением

(3.74)

или в операторной форме

. (3.75)

Передаточная функция

. (3.76)

 

Примеры идеальных дифференцирующих звеньев изображены на рис. 3.25. Единственным идеальным дифференцирующим звеном, которое точно описывается уравнением (3.74), является тахогенератор постоянного тока (рис. 3.25, а), если в качестве входной величины рассматривать угол поворота его ротора a, а в качестве выходной – напряжение якоря U. Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель в режиме дифференцирования (рис. 3.25, б).

 

 

Рис. 3.25. Идеальные дифференцирующие звенья

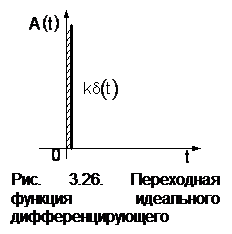
Переходная функция звена при х1 = 1(t); A(t) = k 1’(t) = k d(t) представляет собой импульсную функцию, площадь которой равна k (рис. 3.26). Функция веса представляет собой импульсную функцию второго порядка.

Частотная передаточная функция, её модуль и фаза соответственно равны

w(jw) = k jw; (3.77)

 

A(w) = k w; y = +900 при w > 0;
y = -900 при w < 0. (3.78)

Частотные характеристики изображены на рис. 3.27.

Из амплитудной характеристики видно, что звено пропускает сигнал тем сильнее, чем выше его частота. Это свойство является в автоматических системах часто нежелательным, так как звено может в значительной степени повышать уровень действующих в системе помех, которые, как правило, являются высокочастотными.

 

 

Рис. 3.27. АФЧХ (а), АЧХ (б) и ФЧХ (в) идеального дифференцирующего звена

 

Амплитудно-фазовая характеристика для положительных частот сливается с положительным направлением оси мнимых.

ЛАХ строится по выражению

. (3.79)

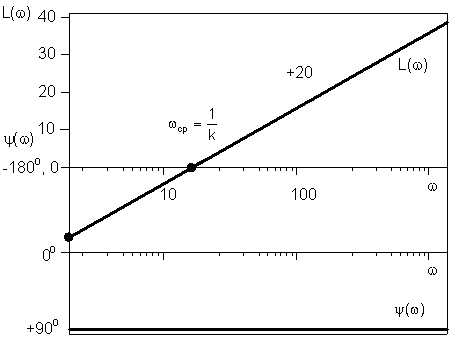
Нетрудно видеть, что ЛАХ представляет собой прямую с положительным наклоном 20 дБ/дек (рис. 3.28). Эта прямая пересекает ось нуля децибел при частоте среза .

 

Рис. 3.28. ЛАХ и ЛФХ идеального дифференцирующего звена

 

ЛФХ представляет собой прямую линию y = +90⁰, параллельную оси частот.