Идеальное интегрирующее звено
Звено описывается уравнением
В операторной форме
Или в другой форме записи Передаточная функция звена
Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Идеальным будет считаться такое звено, у которого можно пренебречь влиянием собственных переходных процессов. Примеры интегрирующих звеньев приведены на рис. 3.19. Наиболее часто в качестве интегрирующего звена используется операционный усилитель в режиме интегрирования (рис. 3.19, а). Интегрирующим звеном является также обычный гидравлический демпфер (рис. 3.19, б). Входной величиной является здесь сила F, действующая на поршень, а выходной – перемещение поршня x.
Рис. 3.19. Идеальные интегрирующие звенья
Так как скорость движения поршня демпфера пропорциональна приложенной силе
где S – коэффициент скоростного сопротивления, то его перемещение будет пропорциональным интегралу от приложенной силы по времени
Передаточная функция демпфера
Переходная функция идеального интегрирующего звена при х1 = 1(t) и нулевых начальных условиях
и функция веса
Временные характеристики изображены на рис. 3.20.
Рис. 3.20. Переходная функция (а) и дельта-функция (б) идеального интегрирующего звена
Частотная передаточная функция, её модуль и фаза соответственно равны w(jw) = k / jw; (3.62) A(w) = k / w; y = -900 при w > 0; y = +900 при w < 0. (3.63) Частотные характеристики изображены на рис. 3.21.
Рис. 3.21. АФЧХ (а), АЧХ (б) и ФЧХ (в) идеального интегрирующего звена
Амплитудная характеристика показывает, что звено пропускает сигнал тем сильнее, чем меньше его частота. При ω = 0 модуль Построение ЛАХ выполняется по выражению
Нетрудно видеть, что ЛАХ представляет собой прямую с отрицательным наклоном 20 дБ/дек, пересекающую ось нуля децибел при частоте среза ω ср = k. ЛФХ представляет собой прямую y = –900, параллельную оси частот.
|

 . (3.54)
. (3.54) . (3.55)
. (3.55) , откуда и получилось название звена. В идеальном интегрирующем звене выходная величина пропорциональна интегралу по времени от входной или скорость изменения выходной величины пропорциональна входной величине звена.
, откуда и получилось название звена. В идеальном интегрирующем звене выходная величина пропорциональна интегралу по времени от входной или скорость изменения выходной величины пропорциональна входной величине звена. . (3.56)
. (3.56)
 , (3.57)
, (3.57)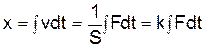 . (3.58)
. (3.58) . (3.59)
. (3.59) (3.60)
(3.60) . (3.61)
. (3.61)

 . Амплитудно-фазовая характеристика для положительных частот сливается с отрицательной частью оси мнимых.
. Амплитудно-фазовая характеристика для положительных частот сливается с отрицательной частью оси мнимых. . (3.64)
. (3.64)


