Апериодическое звено второго порядка
Звено относится к группе позиционных звеньев и описывается уравнением
При этом корни характеристического уравнения
должны быть вещественными, что будет выполняться при условии Т1 ≥ 2 Т2. Левая часть уравнения (3.39) разлагается на множители
где
Передаточная функция звена
Из последнего выражения видно, что апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи k и постоянными времени Т3 и Т4. Примеры апериодических звеньев второго порядка приведены на рис. 3.15. Рассмотрим подробно случай двигателя постоянного тока (рис. 3.15, в). При отсутствии момента нагрузки на валу и при учете переходных процессов в цепи якоря динамика двигателя описывается двумя уравнениями, соответствующими закону равновесия эдс в цепи якоря
и закону равновесия моментов на валу двигателя
где СЕ и СМ – коэффициенты пропорциональности между противо эдс и скоростью вращения и между вращающим моментом и током якоря; J – приведенный момент инерции; L и R – индуктивность и сопротивление цепи якоря.
Рис. 3.15. Апериодические звенья второго порядка
Решая уравнения (3.44) и (3.45) совместно, получим передаточную функцию двигателя постоянного тока при управлении напряжением якоря
где электромеханическая постоянная времени
и электромагнитная постоянная времени якорной цепи
Для того чтобы корни знаменателя в (3.46) были вещественными и передаточную функцию можно было представить в виде (3.43), необходимо выполнение условия Переходная функция получается путем решения дифференциального уравнения (3.39) при x1 = 1(t) и нулевых начальных условиях, то есть при t = 0; x2 = 0 и
Функция веса
Временные характеристики звена изображены на рис. 3.16 (для определенности принято
Рис. 3.16. Переходная функция (а) и дельта-функция (б) апериодического звена второго порядка
На переходной характеристике показано построение, позволяющее по экспериментальным данным определять постоянные времени Т3 и Т4. Частотная передаточная функция согласно (3.43), её модуль и фаза соответственно равны
Амплитудная, фазовая и амплитудно-фазовая характеристики показаны на рис. 3.17. На амплитудно-фазовой характеристике отмечены три характерные точки: ω = 0;
Рис. 3.17. АФЧХ (а), АЧХ (б) и ФЧХ (в) апериодического звена второго порядка
Построим теперь логарифмические характеристики (рис. 3.18). Для этой цели проведем вертикальные пунктирные прямые при сопрягающих частотах w3 = 1 / T3 и w4 = 1 / T4. Будем считать, что T3 > T4 и w3 < w4. ЛАХ определяется выражением
Для частот, меньших, чем сопрягающая частота ω 3 (а значит и меньших, чем частота ω 4), будет справедливым Для частот ω 3< ω < ω 4 будет справедливым Для частот Ломаная линия а–b–с–d представляет собой асимптотическую ЛАХ. Действительная ЛАХ показана пунктиром. Она будет расходиться с асимптотической ЛАХ в местах изломов на 3 дБ.
Рис. 3.18. ЛАХ и ЛФХ апериодического звена второго порядка
ЛФХ получается суммированием двух слагаемых (см. второе уравнение (3.52)). Каждое слагаемое дает фазовую характеристику, совпадающую с ЛФХ апериодического звена первого порядка (рис. 3.18). В результате суммирования получаем ЛФХ, ордината которой соответствует
|

 . (3.39)
. (3.39) (3.40)
(3.40) , (3.41)
, (3.41) . (3.42)
. (3.42) . (3.43)
. (3.43) (3.44)
(3.44) , (3.45)
, (3.45)
 , (3.46)
, (3.46) (3.47)
(3.47) . (3.48)
. (3.48) .
.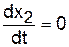
 . (3.49)
. (3.49) . (3.50)
. (3.50)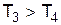 ).
).
 ; (3.51)
; (3.51) . (3.52)
. (3.52) .
.
 ..(3.53)
..(3.53) и
и 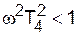 . Поэтому в этой области можно допустить L(w)» 20 lgk. Этому выражению соответствует прямая а–b на рис. 3.18.
. Поэтому в этой области можно допустить L(w)» 20 lgk. Этому выражению соответствует прямая а–b на рис. 3.18. и
и  . Поэтому в этой области можно принять L(w)» 20 lg(k / wT3), чему соответствует прямая с отрицательным наклоном 20 дБ/дек (прямая b-с на рис. 3.18) (подразд. 3.4, п. 2).
. Поэтому в этой области можно принять L(w)» 20 lg(k / wT3), чему соответствует прямая с отрицательным наклоном 20 дБ/дек (прямая b-с на рис. 3.18) (подразд. 3.4, п. 2).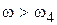 имеем соответственно
имеем соответственно  , а также L(w)» 20 lg(k / wT3T4), чему соответствует прямая с отрицательным наклоном 40 дБ/дек (прямая с–d на рис. 3.18) (см. подразд. 3.4, п. 3).
, а также L(w)» 20 lg(k / wT3T4), чему соответствует прямая с отрицательным наклоном 40 дБ/дек (прямая с–d на рис. 3.18) (см. подразд. 3.4, п. 3).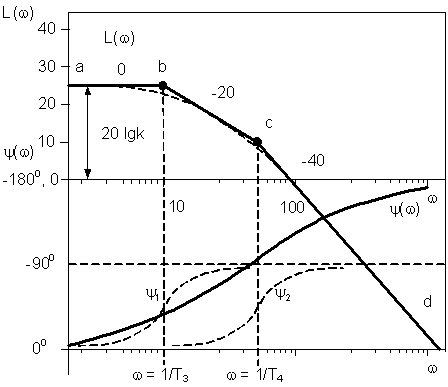
 при
при  и
и  .
.


