Инерционное интегрирующее звено
Звено описывается дифференциальным уравнением:
или
Передаточная функция звена
Примером такого звена является двигатель постоянного тока, если в качестве входной величины рассматривать напряжение на якоре, а в качестве выходной – угол поворота вала двигателя. Интегрирующее звено с замедлением можно представить как совокупность двух звеньев, включенных последовательно, – идеального интегрирующего и апериодического звена первого порядка. Для нахождения переходной характеристики удобно передаточную функцию представить в виде суммы
что позволяет представить решение дифференциального уравнения в виде суммы решения для идеального интегрирующего звена и решения для апериодического звена первого порядка, которые были рассмотрены ранее. В результате получаем переходную функцию звена при х1 = 1(t) и нулевых начальных условиях
и функцию веса
Временные характеристики изображены на рис. 3.22. На характеристиках изображены построения, с помощью которых можно по экспериментальной характеристике определить параметры звена. Частотная передаточная функция, её модуль и фаза равны соответственно
Рис. 3.22. Переходная функция (а) и дельта-функция (б) инерционного интегрирующего звена
Амплитудная, фазовая и амплитудно-фазовая характеристики изображены на рис. 3.23. Из характеристик видно, что звено также пропускает сигналы тем сильнее, чем меньше их частота. В отличие от предыдущего звена фазовый сдвиг равен –900 только на очень низких частотах. С ростом частоты фазовый сдвиг
Рис. 3.23. АФЧХ (а), АЧХ (б) и ФЧХ (в) инерционного интегрирующего звена
Построение ЛАХ выполняется по выражению
Сначала проводится вертикальная линия (рис. 3.24), соответствующая сопрягающей частоте w = 1/T. При частотах, меньших, чем сопрягающая, можно приближенно положить
Рис. 3.24. ЛАХ и ЛФХ инерционного интегрирующего звена
Это будет аналогичная предыдущему звену прямая с отрицательным наклоном 20 дБ/дек, имеющая частоту среза ω ср = k. Прямую можно провести в области малых частот до сопрягающей частоты (прямая а–b). Правее сопрягающей частоты, то есть при частотах w > 1/T, выражение (2.73), можно пренебречь единицей по сравнению с ЛФХ строится суммированием постоянного фазового сдвига y1 = –900 и переменного фазового сдвига y2 = –аrctg ω Т. При сопрягающей частоте имеем y2 = –450 и y = y1 + y2 = –1350. Из логарифмических характеристик видно, что звено приближается к идеальному интегрирующему звену при частотах, меньших сопрягающей, и тем точнее, чем меньше рабочая частота по сравнению с сопрягающей.
|

 (3.65)
(3.65) . (3.66)
. (3.66)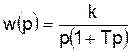 . (3.67)
. (3.67) , (3.68)
, (3.68)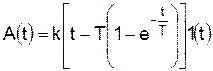 (3.69)
(3.69)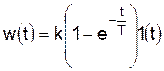 . (3.70)
. (3.70) ; (3.71)
; (3.71)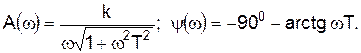 (3.72)
(3.72)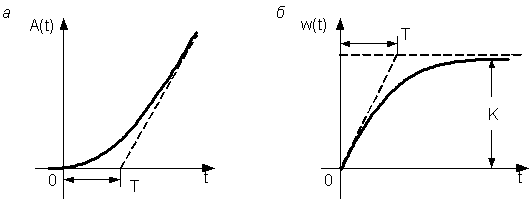
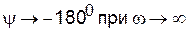 .
.
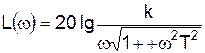 . (3.73)
. (3.73) .
.
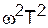 . Поэтому вместо (2.73) можно принять приближенное выражение
. Поэтому вместо (2.73) можно принять приближенное выражение  . Этому выражению соответствует прямая с отрицательным наклоном 40 дБ/дек. Поэтому правее точки b нужно провести прямую с наклоном 40 дБ/дек (прямая b–c). Ломанная прямая а–b–c представляет собой асимптотическую ЛАХ. Действительная ЛАХ (показана пунктиром) будет иметь наибольшее отклонение от асимптотической в точке b, то есть при сопрягающей частоте. Ошибка в этой точке будет составлять 3 дБ, то есть в линейном масштабе ошибка амплитуды будет в
. Этому выражению соответствует прямая с отрицательным наклоном 40 дБ/дек. Поэтому правее точки b нужно провести прямую с наклоном 40 дБ/дек (прямая b–c). Ломанная прямая а–b–c представляет собой асимптотическую ЛАХ. Действительная ЛАХ (показана пунктиром) будет иметь наибольшее отклонение от асимптотической в точке b, то есть при сопрягающей частоте. Ошибка в этой точке будет составлять 3 дБ, то есть в линейном масштабе ошибка амплитуды будет в  раз меньше. По мере удаления от сопрягающей частоты влево и вправо действительная ЛАХ будет сливаться с асимптотами, то есть прямыми а–b и b–с.
раз меньше. По мере удаления от сопрягающей частоты влево и вправо действительная ЛАХ будет сливаться с асимптотами, то есть прямыми а–b и b–с.


