Общий метод составления исходных уравнений
Системы автоматического регулирования в большинстве случаев являются сложными устройствами, динамика которых описывается совокупностью дифференциальных уравнений. Для получения этой совокупности необходимо составить дифференциальное уравнение для каждого элемента автоматической системы так, чтобы общее число уравнений было не меньше, чем число независимых обобщенных координат, определяющих состояние системы. При составлении дифференциального уравнения каждого элемента необходимо прежде всего выявить физический закон, определяющий его поведение. Таким законом может быть, например, закон сохранения вещества (объекты регулирования уровня, давления); закон сохранения энергии (объекты регулирования температуры); закон равновесия моментов (объекты регулирования скорости или угла поворота); закон равновесия электродвижущих сил (электрические цепи) и другие основные законы физики. Математическое выражение соответствующего физического закона и является исходным дифференциальным уравнением данного элемента автоматической системы. Для электродвигателя закон равновесия моментов на его валу может быть записан в следующем виде:
где J и Ω – приведенный момент инерции и угловая скорость двигателя; МВ – вращающий момент двигателя; МТ – тормозной момент внешних сил (момент нагрузки). После записи дифференциального уравнения необходимо определить факторы, от которых зависят переменные, входящие в это уравнение. Необходимо установить, от каких величин, какими выражениями определяются вращающий момент двигателя МВ и тормозной момент МТ на его валу. Нужно также выяснить, является ли приведенный момент инерции постоянной величиной или он изменяется в функции какой-то переменной (например в функции угла поворота двигателя). Так, например, если исследуется двигатель постоянного тока с параллельным возбуждением, то вращающий момент будет пропорциональным произведению постоянного потока Ф = соnst и тока якоря ІЯ
Момент нагрузки может быть постоянным или зависеть от какой-то величины, например, от скорости вращения двигателя, его угла поворота, времени и т.д. Так, если момент пропорционален квадрату скорости (вентиляционная нагрузка) МТ = k Ω 2, то при постоянстве приведенного момента инерции J = const уравнение (4.1) будет иметь следующий вид:
Дальнейшим шагом является линеаризация полученных уравнений в соответствии рассмотренным далее методом, если линеаризация вообще является допустимой. Обычно достаточные признаки возможности производить линеаризацию заключаются в отсутствии разрывных, неоднозначных или резко изгибающихся характеристик и в справедливости уравнений в течение всего интервала времени регулирования. После нахождения совокупности дифференциальных уравнений системы целесообразно для упрощения представить их в операторном виде и затем решать совместно относительно интересующей величины. Обычно система уравнений решается относительно отклонения регулируемой величины от заданного значения (ошибки – x(t)) или относительно самой регулируемой величины Х(t). Первый случай встречается чаще, так как исследование изменения ошибки, как правило, является более важным. В этом случае получается дифференциальное уравнение, которое иногда называется дифференциальным уравнением движения регулятора,
Полином D(p) степени n оператора
где а0 – аn в линеаризованной системе представляют собой постоянные коэффициенты. Полином С(р) той же степени
где С0 – Сn – постоянные коэффициенты, определяют влияние управляющего воздействия Y(t) на характер изменения ошибки х(t). Выражение Полиномы МК(р) определяют влияние возмущающих воздействий FK(t) на характер изменения ошибки х(t). Если для какого-то возмущающего воздействия Из (4.4) вытекает, что ошибка системы автоматического регулирования может быть представлена в виде суммы двух составляющих. Первая составляющая определяется наличием управляющего воздействия Y(t). Вторая составляющая определяется наличием возмущающих воздействий. В системах автоматической стабилизации ошибка сводится только ко второй составляющей, то есть она определяется только наличием возмущающих воздействий. При решении системы дифференциальных уравнений относительно регулируемой величины Х(t) получается так называемое уравнение движения регулируемого объекта при наличии автоматического регулирования. Это уравнение может быть получено в результате подстановки выражения для ошибки х(t) = Y(t) – X(t) в уравнение (4.4). В результате имеем:
где полином В(p) определяется выражением
Степень полинома B(p) – m, причем (m ≤ n)
Как и ранее в системах автоматической стабилизации при Y(t) = const можно при соответствующем выборе начала отсчета получить Y(t) = 0, что упрощает выражение (4.7). При заданных функциях времени в правой части дифференциальных уравнений (4.4) и (4.7) эти уравнения могут быть решены (проинтегрированы) относительно искомых функций времени, то есть может быть найдено изменение ошибки регулирования во времени х(t) из (4.4) и движение регулируемого объекта вместе с регулятором Х(t) – из (4.7).
4.2. Передаточные функции систем автоматического
Предположим вначале, что чувствительный элемент (ЧЭ) отсоединен от объекта регулирования (ОР) и рассмотрим так называемую разомкнутую систему автоматического регулирования. Регулирующее воздействие, которое прикладывает исполнительный элемент (ИЭ) к регулируемому объекту, определяется выражением
где х – рассогласование на выходе чувствительного элемента; wрег(p) – передаточная функция цепи регулирования. Регулируемая величина может быть найдена из выражения
где wF(p) – передаточная функция регулируемого объекта по регулирующему воздействию; wK(p) – передаточная функция регулируемого объекта по возмущающему воздействию FK. Подставляя (4.8) в (4.9), имеем:
В 4.10 введена так называемая передаточная функция разомкнутой системы
которая равна отношению регулируемой величины к ошибке при внешних возмущениях, равных нулю. При этих условиях передаточная функция разомкнутой системы дает связь между регулируемой величиной и ошибкой
Рассмотрим теперь замкнутую систему, то есть предположим, что чувствительный элемент соединен с регулируемым объектом. В этом случае можно использовать уравнение замыкания x = Y – X. (4.13) Решая (4.10) и (4.13) совместно, имеем для регулируемой величины
а для ошибки получим такое выражение
Выражение
называется передаточной функцией замкнутой системы или главным оператором. Передаточная функция замкнутой системы дает связь между регулируемой величиной и управляющим воздействием при равенстве нулю возмущающих воздействий
Передаточная функция разомкнутой системы может быть представлена в виде дробно-рациональной функции от оператора p. В результате сравнения формул (4.4) и (4.7) с формулами (4.14) и (4.15) можно получить следующее выражение для передаточной функции разомкнутой системы:
где В(p) и D(p) – полиномы от оператора, совпадающие с соответствующими полиномами в (4.4) и (4.7). Характеристический полином системы
Приравнивание нулю характеристического полинома дает характеристическое уравнение системы
Оно может быть записано в более удобной форме, которая непосредственно получается из (4.4) и (4.7), так как характеристическое уравнение системы есть знаменатель операторного выражения, приравненный нулю:
Для полиномов МК(p), входящих в формулы (4.4) и (4.7), можно положить следующее соотношение:
Из рассмотренного видно, что знание передаточной функции разомкнутой системы позволяет легко найти выражение для ошибки и регулируемой величины в функции управляющего и возмущающих воздействий.
|

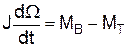 , (4.1)
, (4.1)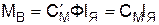 . (4.2)
. (4.2) . (4.3)
. (4.3)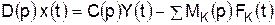 . (4.4)
. (4.4)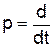 характеризует свободное движение регулируемого объекта с регулятором. Он называется характеристическим полиномом и может быть представлен в виде
характеризует свободное движение регулируемого объекта с регулятором. Он называется характеристическим полиномом и может быть представлен в виде , (4.5)
, (4.5) , (4.6)
, (4.6)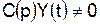 только в случае программного регулирования и в следящих системах. В системах автоматической стабилизации
только в случае программного регулирования и в следящих системах. В системах автоматической стабилизации 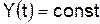 . Поэтому всегда можно выбрать начало отсчета так, чтобы
. Поэтому всегда можно выбрать начало отсчета так, чтобы  , что упрощает выражение (4.4).
, что упрощает выражение (4.4). полином
полином 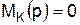 , то система автоматического регулирования является инвариантной относительно этого воздействия.
, то система автоматического регулирования является инвариантной относительно этого воздействия.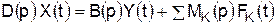 , (4.7)
, (4.7)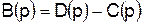 . (4.8)
. (4.8) . (4.9)
. (4.9)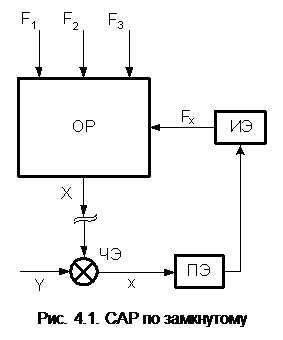 Записанные выше дифференциальные уравнения САР (4.4) и (4.7) могут быть легко получены на основании понятия передаточной функции, которое было введено ранее (см. подразд. 3.1). Рассмотрим систему автоматического регулирования по замкнутому циклу (рис. 4.1).
Записанные выше дифференциальные уравнения САР (4.4) и (4.7) могут быть легко получены на основании понятия передаточной функции, которое было введено ранее (см. подразд. 3.1). Рассмотрим систему автоматического регулирования по замкнутому циклу (рис. 4.1).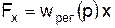 , (4.8)
, (4.8)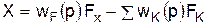 , (4.9)
, (4.9)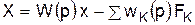 . (4.10)
. (4.10)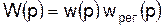 , (4.11)
, (4.11)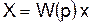 . (4.12)
. (4.12) , (4.14)
, (4.14)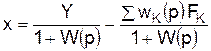 . (4.15)
. (4.15)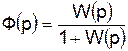 (4.16)
(4.16)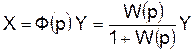 . (4.17)
. (4.17)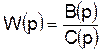 , (4.18)
, (4.18)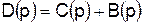 . (4.19)
. (4.19)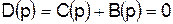 . (4.20)
. (4.20)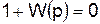 . (4.21)
. (4.21)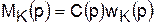 . (4.22)
. (4.22)


