Составление уравнений на основе типовых звеньевНахождение основных уравнений системы автоматического регулирования (4.14) и (4.15) во многих случаях может быть значительно облегчено использованием понятия динамических звеньев. Динамические звенья были подробно рассмотрены в разд. 3. Часто систему автоматического регулирования можно разбить на комбинацию динамических звеньев с определенными «типовыми» передаточными функциями. Эти звенья могут соединяться друг с другом различным образом. Наиболее часто встречаются следующие соединения звеньев.
1. Последовательное соединение звеньев (рис. 4.2).
Рис. 4.2. Последовательное соединение звеньев
В этом случае результирующая передаточная функция равна произведению передаточных функций отдельных звеньев
Следует подчеркнуть, что это правило будет справедливым только в том случае, когда соединение выхода предыдущего звена с входом последующего не меняет исходных уравнений каждого звена и, следовательно, его передаточной функции. Если при соединении двух звеньев наблюдается влияние одного звена на другое, в результате которого меняются исходные уравнения какого-то звена, то такое соединение двух звеньев должно рассматриваться как новое самостоятельное звено со своей передаточной функцией. 2. Параллельное соединение звеньев (рис. 4.3).
Для этого правила остаются справедливыми замечания, сделанные ранее относительно взаимного влияния звеньев. 3. Обратные связи (рис. 4.4). Обратная связь может быть положительной, если сигнал х3 с выхода второго звена суммируется с сигналом х1 на выходе первого звена, и отрицательной, если он вычитается. Для нахождения результирующей передаточной функции такой комбинации звеньев запишем следующие соотношения:
где знак плюс относится к положительной, а знак минус – к отрицательной обратной связи. Решая эти уравнения совместно, имеем
Здесь знак минус относится к положительной, а знак плюс – к отрицательной обратной связи. При использовании понятия динамических звеньев обычно наиболее просто находится передаточная функция разомкнутой системы (см. рис. 4.1). Затем по ранее рассмотренным правилам легко находится уравнение системы автоматического регулирования. При анализе для системы автоматического регулирования необходимо составить так называемую структурную схему (рис. 4.5), представляющую собой совокупность динамических звеньев и связи между ними.
Рис. 4.5. Пример структурной схемы САР
Такая структурная схема часто является весьма простой и её составление не представляет особого труда. Однако в некоторых случаях составление структурной схемы сопряжено с большими трудностями и может быть сделано только на основе детального анализа исходных дифференциальных уравнений системы регулирования. В этом случае структурная схема не облегчает нахождения основных уравнений системы, но и здесь она остается весьма ценной, так как на ней в наглядной форме представлены все узлы исследуемой системы и все существующие между ними связи. Это может оказаться полезным во всех дальнейших исследованиях. На рис. 4.5 изображен пример системы автоматического регулирования (структурная схема). Передаточная функция разомкнутой системы в случае размыкания обратной связи будет иметь вид:
Для нахождения передаточной функции разомкнутой системы можно разомкнуть систему в другом месте, например в точках а, b, с или d. После получения передаточной функции разомкнутой системы по выражению (4.16) получают передаточную функцию замкнутой системы, а по формулам (4.14) или (4.15) – дифференциальные уравнения САР.
Контрольные вопросы 1. Изложите классический метод составления дифференциальных уравнений. 2. Назовите виды дифференциальных уравнений САР. 3. Дайте определение характеристическому полиному. 4. Назовите передаточные функции САР. 5. Опишите методику составления дифференциальных уравнений системы на основе типовых динамических звеньев.
5. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ систем автоматического
|
. (4.23)
Так как сигналы на выходе всех звеньев складываются, то результирующая передаточная функция в этом случае равна сумме передаточных функций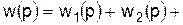
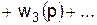. (4.24)
, (4.25)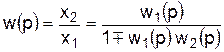
. (4.26)
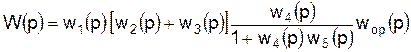. (4.27)
