При построении матрицы руководствуются следующими правилами
1. По диагонали от левого верхнего до правого нижнего углов выписываются все коэффициенты по порядку от а1 до аn. 2. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. 3. В случае отсутствия данного коэффициента, если индекс меньше нуля или больше n, на месте его пишется нуль.
Критерий устойчивости сводится к тому, что при а0> 0 должны быть больше нуля все n определителей Гурвица, полученных из квадратной матрицы коэффициентов. Определители Гурвица составляются по следующему правилу (5.12).
Последний определитель Δ n включает в себя всю матрицу. Но так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то последний определитель выражается через предпоследний следующим образом: Δ n = аn Δ n-1. (5.16) Но в устойчивой системе предпоследний определитель тоже должен быть больше нуля, поэтому условие положительности последнего определителя сводится к аn > 0. Условия нахождения системы на границе устойчивости можно получить, приравнивая нулю последний определитель Δ n = 0, при положительности всех остальных определителей. Как следует из (5.16), это условие распадается на два: аn = 0 и Δ n-1 = 0. Первое условие соответствует границе устойчивости первого типа (апериодическая граница устойчивости) и второе – границе второго типа (колебательная граница устойчивости). Развертывая определители, фигурирующие в общей формулировке критерия устойчивости Гурвица, можно получить в виде частных случаев критерии устойчивости для системы первого, второго, третьего, четвертого и более высоких порядков. Частные случаи критерия Гурвица.
|
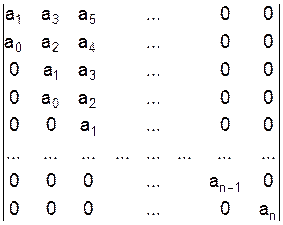(5.12)
; (5.13)
; (5.14)
. (5.15)
