Метод фазовой плоскости
Метод изображения процессов с помощью фазовых траекторий в принципе может использоваться для систем, описываемых дифференциальным уравнением любого порядка. Однако эти траектории должны рассматриваться в n-мерном фазовом пространстве, где n – порядок дифференциального уравнения. Ввиду серьезных трудностей, возникающих при рассмотрении n-мерного пространства при n > 3, метод фазовых траекторий находит применение только для систем второго порядка, где пространство превращается в плоскость, и в некоторых случаях для систем третьего порядка. Рассмотрим применение этого метода для систем второго порядка, когда фазовые траектории располагаются на фазовой плоскости. Фазовая плоскость это координатная плоскость, где по оси абсцисс откладывается сама переменная, для которой исследуется переходный процесс, а по оси ординат – скорость изменения (первая производная) этой переменной (иногда другая переменная, характеризующая процесс в системе во втором порядке).
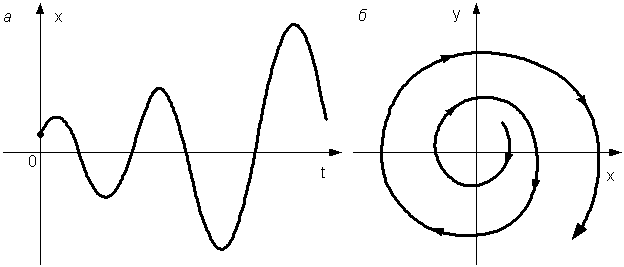
Если в исследуемой системе протекает некоторый процесс, то изображающая точка будет двигаться по плоскости, прочерчивая кривую, которая называется фазовой траекторией. Направление движения изображающей точки принято обозначать на траектории стрелками. Основные свойства фазовой траектории. 1. В верхней полуплоскости направление движения изображающей точки может быть только слева направо. Это вытекает из того, что в верхней полуплоскости 2. Фазовая траектория может пересекать ось абсцисс только под прямым углом. Это вытекает из того, что в точке пересечения производная у = 3. Замкнутым фазовым траекториям соответствуют периодические процессы. Рассмотрим изображение типичных процессов на фазовой плоскости. 1. Затухающий колебательный процесс. Начальная точка процесса (рис. 9.2, а) имеет некоторые определенные значения: x = x0 и
Рис. 9.2. Затухающий колебательный процесс
Затухающие колебания свидетельствуют об устойчивости этого равновесного состояния. Начало координат фазовой плоскости в этом случае является особой точкой плоскости, называемой устойчивым фокусом (рис. 9.2, б). 2. Расходящийся колебательный процесс. Аналогичным рассуждением можно показать, что фазовым портретом расходящихся колебаний (рис. 9.3, а) будет спираль, удаляющаяся от начала координат (рис. 9.3, б).
Рис. 9.3. Расходящийся колебательный процесс
Если этот процесс имеет место при сколь угодно малом начальном отклонении, то это свидетельствует о неустойчивости равновесного состояния (х = 0, у = 0). Начало координат фазовой плоскости в этом случае называется неустойчивым фокусом. 3. Апериодический затухающий процесс (рис. 9.4, а) на фазовой плоскости изобразится в виде кривой, которая вливается в начало координат (рис. 9.4, б), причем изображающая точка движется по этой кривой так, что к началу координат она приближается при
Рис. 9.4. Затухающий апериодический процесс
4. Апериодический расходящийся процесс (рис. 9.5, а) изобразится в виде кривой, удаляющейся на фазовой плоскости от начала координат (рис. 9.5, б). Если процесс расходится при сколь угодно малом начальном отклонении, то начало координат называется неустойчивым узлом.
Рис. 9.5. Расходящийся апериодический процесс
5. Периодический колебательный процесс (рис. 9.6, а) изобразится на фазовой плоскости в виде замкнутой кривой, циклом (рис. 9.6, б). Для синусоидальных колебаний цикл имеет вид эллипса, который подбором масштабов по осям может быть превращен в окружность.
Рис. 9.6. Периодический процесс
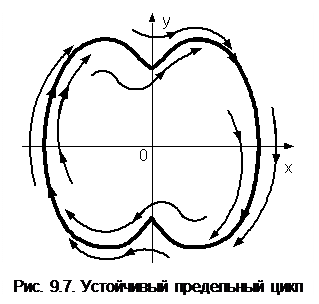
6. Устойчивые автоколебания. Могут существовать такие условия, когда на фазовой плоскости присутствует замкнутая фазовая траектория (рис. 9.7), к которой в пределе стремятся все фазовые траектории плоскости. Тогда замкнутая кривая называется устойчивым предельным циклом. В этом случае все фазовые траектории, находящиеся внутри предельного цикла, соответствуют расходящемуся процессу. Эти фазовые траектории в пределе сливаются с замкнутой кривой (предельным циклом). С другой стороны, все фазовые траектории, находящиеся снаружи предельного цикла, соответствуют сходящемуся процессу. При этом фазовые траектории навиваются на замкнутую кривую, в пределе сливаясь с ней. Такая картина соответствует устойчивым автоколебаниям в системе, так как любая фазовая траектория в конце концов сольется с предельным циклом, что соответствует периодическому режиму в системе. По кривой предельного цикла можно установить амплитуду автоколебаний, то есть максимальное значение исследуемой величины.
Внутри такого предельного цикла фазовые траектории соответствуют сходящемуся процессу. Поэтому, если начальная точка исследуемого переходного процесса М0(х0, Снаружи неустойчивого предельного цикла фазовые траектории соответствуют расходящемуся процессу. Поэтому, если начальная точка процесса М0(х0, Из изложенного следует, что понятия устойчивости в нелинейных и линейных системах сильно отличаются друг от друга. Устойчивость линейной системы зависит от структуры и соотношения параметров и не зависит от начальных условий.Устойчивость нелинейной системы может зависеть также и от начальных условий. Периодический режим, соответствующий неустойчивому предельному циклу, не может долго существовать, и фазовая траектория в зависимости от случайных воздействий пойдет внутрь или наружу предельного цикла. Так как процесс в реальной системе не может расходиться бесконечно далеко, и где-то должно произойти ограничение, то при наличии неустойчивого предельного цикла на фазовой плоскости должен обязательно существовать больший по размерам устойчивый предельный цикл, к которому и будут стремиться фазовые траектории, находящиеся снаружи неустойчивого предельного цикла. А.А. Андроновым был разработан метод точечных преобразований [1], который является соединением методов припасовывания и фазовых траекторий. Он уменьшает объем построений и вводит в рассмотрение также и время протекания процесса, которое в явном виде отсутствует на фазовой плоскости. Для тех случаев, когда затруднительно найти в явном виде уравнения фазовых траекторий, используется приближенный метод их построения, который носит название метода изоклин [1].
Контрольные вопросы 1. Дайте понятие о нелинейных САР. 2. Перечислите методы исследования процессов в нелинейных САР. 3. Изложите метод фазовой плоскости. 4. Перечислите свойства фазовых траекторий. 5. Дайте понятие об устойчивости нелинейных систем.
заключение Системы автоматизированного управления являются важнейшими элементами электроподвижного состава, предназначенными для регулирования скорости и управления процессом движения в режимах тяги и электрического торможения. При их помощи машинист или автоматическое устройство реализует необходимые тяговые и тормозные характеристики ЭПС и, в конечном итоге, выполняет график движения. Современные системы управления используют последние достижения автоматики и информационной электроники. Изучив дисциплину, студент должен знать: принципы автоматического регулирования; временные, частотные и логарифмические частотные характеристики типовых динамических звеньев; методы аналитической и графической линеаризации; методы математического описания систем автоматического регулирования (САР) с помощью передаточных функций; алгебраические и частотные критерии оценки устойчивости линейных систем; методы и критерии исследования качества процесса регулирования; методы инженерного синтеза САР; методы исследования процессов, протекающих в нелинейных САР; способы исследования процессов, протекающих в импульсных САР. Кроме того, студент должен уметь: использовать математический аппарат для описания САР; пользоваться методикой построения частотных характеристик; оценивать устойчивость проектируемой системы; исследовать переходные процессы; оценивать качество процесса регулирования; находить пути повышения устойчивости и улучшения показателей качества регулирования. Освоение настоящей дисциплины позволит будущему специалисту разобраться в процессах, протекающих в системах автоматического регулирования, применяемых на современном ЭПС, а также в вопросах разработки, проектирования и исследования различных систем автоматического управления.
|

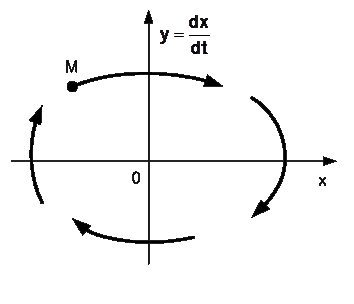 На рис. 9.1 изображена фазовая плоскость. По оси абсцисс откладывается исследуемая величина х, а по оси ординат – ее производная
На рис. 9.1 изображена фазовая плоскость. По оси абсцисс откладывается исследуемая величина х, а по оси ординат – ее производная 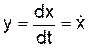 . Состояние системы второго порядка полностью определяется заданием этих двух координат. Каждому состоянию системы соответствует определенная точка на фазовой плоскости, например точка М на рис. 9.1. Эта точка называется изображающей точкой.
. Состояние системы второго порядка полностью определяется заданием этих двух координат. Каждому состоянию системы соответствует определенная точка на фазовой плоскости, например точка М на рис. 9.1. Эта точка называется изображающей точкой. > 0 и величина х должна возрастать. В нижней полуплоскости изображающая точка может двигаться только справа налево.
> 0 и величина х должна возрастать. В нижней полуплоскости изображающая точка может двигаться только справа налево.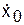 = у0. На фазовой плоскости (рис. 9.2, б) она изобразится определенной точкой М0(х0, у0). В начальной части процесса до точки 1 величина х увеличивается, а производная
= у0. На фазовой плоскости (рис. 9.2, б) она изобразится определенной точкой М0(х0, у0). В начальной части процесса до точки 1 величина х увеличивается, а производная 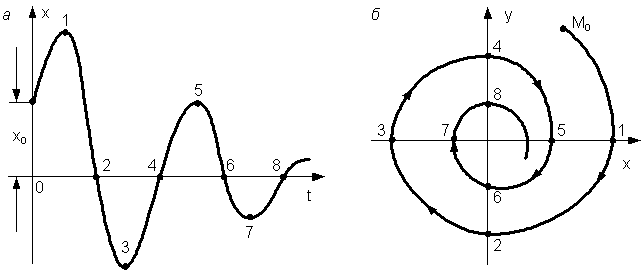
 . Начало координат называется тогда устойчивым узлом.
. Начало координат называется тогда устойчивым узлом.

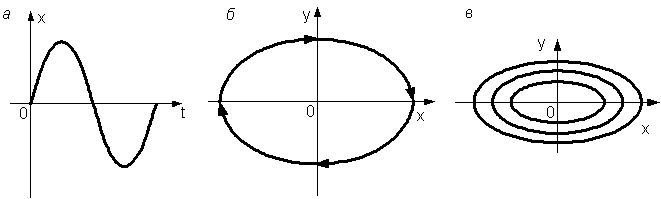
 Для несинусоидальных колебаний цикл имеет вид произвольной замкнутой кривой. В том случае, когда циклы окружают начало координат (рис. 9.6, в), приближаясь к нему бесконечно близко, оно называется особой точкой «центр».
Для несинусоидальных колебаний цикл имеет вид произвольной замкнутой кривой. В том случае, когда циклы окружают начало координат (рис. 9.6, в), приближаясь к нему бесконечно близко, оно называется особой точкой «центр».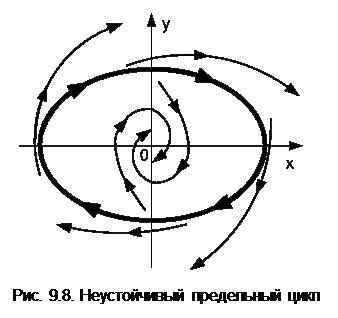 7. Неустойчивые автоколебания. Могут существовать такие условия, когда на фазовой плоскости присутствует замкнутая фазовая траектория (рис. 9.8), от которой внутрь и наружу расходятся фазовые траектории. Эта замкнутая фазовая траектория называется неустойчивым предельным циклом.
7. Неустойчивые автоколебания. Могут существовать такие условия, когда на фазовой плоскости присутствует замкнутая фазовая траектория (рис. 9.8), от которой внутрь и наружу расходятся фазовые траектории. Эта замкнутая фазовая траектория называется неустойчивым предельным циклом.


