Динамический синтез и анализ движения машины
При кинематическом исследовании механизма скорость движения ведущего звена условно была принята постоянной. В действительности кинематические параметры являются функцией действующих в механизме внешних сил и масс подвижных звеньев, и определение истинного закона движения механизма требует специального расчета, т.е. динамического исследования механизма. При динамических исследованиях машин и механизмов, как правило, с целью упрощения производится идеализация реальной системы, которая сводится к построению динамической модели, позволяющей абстрагироваться от конкретной конструкции, но при этом сохранить неизменными основные динамические свойства системы. В первом приближении часто ограничиваются исследованием систем с одной степенью свободы, считая условно, что все звенья механизмов, входящих в состав машины, являются абсолютно твердыми телами. Для систем с одной степенью свободы в качестве динамической модели принимается вращающееся статически уравновешенное твердое тело или точечные поступательно движущиеся или вращающиеся массы. Причем чаще всего модель размещается на входном звене основного механизма машины, так как именно закон движения входного звена необходимо определять в первую очередь при динамическом исследовании. При построении динамической модели необходимо соблюдать следующие условия динамической эквивалентности. 1. Силы или моменты сил, приложенные к динамической модели, производят на возможном перемещении работу, равную (за равный промежуток времени) сумме работ всех сил и моментов, действующих на механизм на их возможных перемещениях. Мгновенная мощность, развиваемая силами или моментами на динамической модели, равна сумме мощностей, развиваемых всеми силами и моментами, действующими на механизм. 2. Динамическая модель должна обладать условной массой или моментом инерции массы, которые при скорости модели способны развить кинетическую энергию, равную сумме кинетических энергий, развиваемых всеми звеньями механизма, т. е. равную кинетической энергии механизма. Звено, на котором размещается модель, принято называть звеном приведения; его массу или момент инерции — приведенной массой или приведенным моментом инерции; действующие на него силы и моменты сил — приведенными силами или приведенными моментами сил (обобщенными силами). Всякий механизм обладает инерционностью, выраженной величиной его приведенного момента инерции
На практике приведенный момент инерции механизма изменяют за счет первого слагаемого. На валу звена приведения всегда можно расположить добавочную массу, выполняемую обычно в виде махового колеса и называемую маховиком. Подбирая момент инерции маховика, можно придать величине Определение Исходя из теоремы об изменении кинетической энергии, можно записать
В общем случае кинетическая энергия механизма может быть выражена следующим образом:
где
Кинетическая энергия первой группы звеньев может быть определена
В связи с неравномерностью вращения звена приведения величина кинетической энергии первой группы звеньев колеблется от
Если принять, что то Решая (*) относительно
Известно, что изменение кинетической энергии механизма происходит за счет работы всех сил и моментов, приложенных к механизму, поэтому запишем
где
После алгебраического суммирования графиков работ Полагая
Таким образом, график Определив значения
|

 . Известно, что чем более инертна материальная система, тем значительнее она сопротивляется изменениям своей скорости, вызываемым действием приложенных к ней сил. Поэтому, чтобы заставить вал механизма вращаться с неравномерностью, не превышающей допустимой нормы, нужно сделать инерционность механизма достаточно большой. Приведенный момент инерции механизма всегда можно представить в виде суммы двух слагаемых
. Известно, что чем более инертна материальная система, тем значительнее она сопротивляется изменениям своей скорости, вызываемым действием приложенных к ней сил. Поэтому, чтобы заставить вал механизма вращаться с неравномерностью, не превышающей допустимой нормы, нужно сделать инерционность механизма достаточно большой. Приведенный момент инерции механизма всегда можно представить в виде суммы двух слагаемых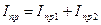
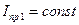 - приведенный момент инерции первой группы звеньев, включающей звено приведения, маховик и звенья, связанные со звеном приведения постоянством передаточного отношения (шкивы ременной передачи, ротор электродвигателя, зубчатые колеса).
- приведенный момент инерции первой группы звеньев, включающей звено приведения, маховик и звенья, связанные со звеном приведения постоянством передаточного отношения (шкивы ременной передачи, ротор электродвигателя, зубчатые колеса).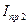 - приведенный момент инерции звеньев, имеющих переменный приведенный момент инерции (шатун, коромысло, ползун и т.д.).
- приведенный момент инерции звеньев, имеющих переменный приведенный момент инерции (шатун, коромысло, ползун и т.д.).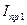 такое значение, при котором вал звена приведения будет вращаться с допустимой степенью неравномерности. Таким образом, динамическое исследование механизма представляет расчет маховика, основное назначение которого состоит в ограничении колебаний угловой скорости в пределах, устанавливаемых величиной коэффициента неравномерности
такое значение, при котором вал звена приведения будет вращаться с допустимой степенью неравномерности. Таким образом, динамическое исследование механизма представляет расчет маховика, основное назначение которого состоит в ограничении колебаний угловой скорости в пределах, устанавливаемых величиной коэффициента неравномерности  .
. , обеспечивающего заданный коэффициент неравномерности движения механизма, может быть выполнено различными методами. Сравнительная простота, наглядность, возможность оценки изменения угловой скорости звена приведения отличает метод профессора Н.И. Мерцалова.
, обеспечивающего заданный коэффициент неравномерности движения механизма, может быть выполнено различными методами. Сравнительная простота, наглядность, возможность оценки изменения угловой скорости звена приведения отличает метод профессора Н.И. Мерцалова. .
.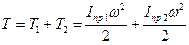 ,
,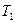 — кинетическая энергия звена приведения, маховика и звеньев, связанных со звеном приведения постоянством передаточного отношения (первая группа звеньев)
— кинетическая энергия звена приведения, маховика и звеньев, связанных со звеном приведения постоянством передаточного отношения (первая группа звеньев) 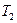 — кинетическая энергия звеньев приведенный момент инерции которых переменен (вторая группа звеньев)
— кинетическая энергия звеньев приведенный момент инерции которых переменен (вторая группа звеньев) 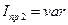 ;
;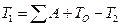
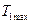 до
до 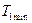 .
.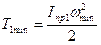 ,
, 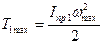
 (*)
(*)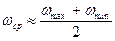 ,
,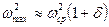 , а
, а 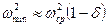 .
. .
. ,
,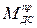 – приведенный момент движущих сил, Н×м;
– приведенный момент движущих сил, Н×м; - приведенный момент сил сопротивления, Н×м;
- приведенный момент сил сопротивления, Н×м;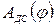 и
и 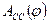 , которые строятся методом графического интегрирования зависимостей
, которые строятся методом графического интегрирования зависимостей  или
или 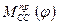 , строится график
, строится график 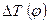 .
.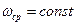 (в связи с тем, что
(в связи с тем, что 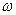 ), найдем
), найдем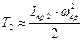
 тождественен графику
тождественен графику  и отличается от него только величиной вычислительного масштаба.
и отличается от него только величиной вычислительного масштаба.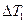 путем вычитания из кривой
путем вычитания из кривой 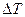 кривой
кривой 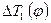 , найдем максимальное изменение его амплитуды, то есть
, найдем максимальное изменение его амплитуды, то есть 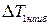 .
.


