В задачу кинематического анализа входит определение законов движения звеньев механизма, вне зависимости от сил действующих на эти звенья.
Построение планов положений
(Приложение 2)
По исходным данным вычерчивается схема механизма в произвольно выбранном масштабе. Масштабный коэффициент 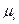 указывает количество единиц изображаемой величины в 1 мм чертежа. При построении планов механизма желательно масштабный коэффициент
указывает количество единиц изображаемой величины в 1 мм чертежа. При построении планов механизма желательно масштабный коэффициент 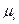 [м/мм] выбирать из следующего ряда: 0.001; 0.002; 0.0025; 0.004; 0.05; 0.08; 0.1 и т.д.
[м/мм] выбирать из следующего ряда: 0.001; 0.002; 0.0025; 0.004; 0.05; 0.08; 0.1 и т.д.
Выбираем масштабный коэффициент 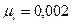 м/мм, тогда отрезок изображающий на чертеже длину
м/мм, тогда отрезок изображающий на чертеже длину  звена
звена  определится:
определится:
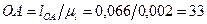 мм.
мм.
Определяем величину отрезков, изображающих длину звеньев 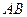 и
и  на чертеже.
на чертеже.
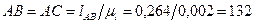 мм.
мм.
Построение начинаем с изображения неподвижных элементов. Наносим на чертеже точку  (ось вращения звена 1) и намечаем траектории точки
(ось вращения звена 1) и намечаем траектории точки 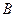 ползуна 3 (
ползуна 3 (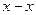 ) и точки
) и точки  ползуна 5 (
ползуна 5 ( ). Далее радиусом
). Далее радиусом  проводим окружность, представляющую собой траекторию точки
проводим окружность, представляющую собой траекторию точки  . На этой окружности на одинаковом расстоянии друг от друга (
. На этой окружности на одинаковом расстоянии друг от друга ( ) наносим положение т.
) наносим положение т.  (0,1,2,3…11). Соединив их отрезками прямых с точкой
(0,1,2,3…11). Соединив их отрезками прямых с точкой  , получим соответствующее положение кривошипа. За начало отсчета принимаем точку
, получим соответствующее положение кривошипа. За начало отсчета принимаем точку 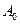 , соответствующую крайнему верхнему положению ползуна
, соответствующую крайнему верхнему положению ползуна 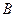 (кривошип
(кривошип  и шатун
и шатун 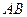 вытянулись в одну прямую).
вытянулись в одну прямую).
Так как данный механизм относится ко второму классу, то положения звеньев в каждой гр. Ассура определим методом засечек.
Положение точки 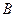 (группа 2,3) определим засечкой, сделанной из т.
(группа 2,3) определим засечкой, сделанной из т.  радиусом
радиусом 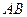 на траектории точки
на траектории точки 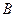 . Соединив точку
. Соединив точку 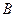 с точкой
с точкой  прямым отрезком, найдем положения звеньев 2 и 3.
прямым отрезком, найдем положения звеньев 2 и 3.
Положение точки  (группа 4,5) определим также засечкой, сделанной из т.
(группа 4,5) определим также засечкой, сделанной из т.  радиусом
радиусом  на траектории точки
на траектории точки  . Соединив точку
. Соединив точку  с точкой
с точкой  отрезком прямой, найдём положение звеньев 4 и 5.
отрезком прямой, найдём положение звеньев 4 и 5.
Таким образом, строятся все 12 положений механизма. При этом заданное положение механизма (координата  ) выделяется основными линиями, а остальные положения вычерчиваются тонкими линиями.
) выделяется основными линиями, а остальные положения вычерчиваются тонкими линиями.
Построение планов скоростей
Построение планов скоростей и ускорений основано на графическом решении векторных уравнений.
Определение линейных скоростей и ускорений точек механизма начинается с механизма первого класса, а затем в порядке присоединения групп Ассура.
Рассмотрим построение плана скоростей для заданного положения механизма  . Модуль скорости точки
. Модуль скорости точки  кривошипа, совершающего вращательное движение относительно стойки, определим
кривошипа, совершающего вращательное движение относительно стойки, определим
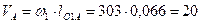 м/с,
м/с,
где 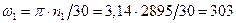 рад/с.
рад/с.
Вектор скорости 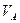 направлен перпендикулярно радиусу кривошипа в сторону его вращения.
направлен перпендикулярно радиусу кривошипа в сторону его вращения.
Масштабный коэффициент 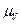 выбираем таким образом, чтобы отрезок
выбираем таким образом, чтобы отрезок  , изображающий скорость
, изображающий скорость 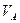 , был не менее 50 мм.
, был не менее 50 мм.
Задаемся масштабным коэффициентом 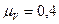 (м×с‾¹)/мм, тогда отрезок
(м×с‾¹)/мм, тогда отрезок  , изображающий скорость
, изображающий скорость 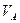 на чертеже, определится
на чертеже, определится
 .
.
 мм.
мм.
Из произвольной точки 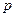 - полюса плана скоростей откладываем в указанном направлении отрезок
- полюса плана скоростей откладываем в указанном направлении отрезок  .
.
Составляем векторное уравнение для определения скорости точки 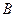 группы Асура (2,3):
группы Асура (2,3):
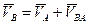 .
.
В этом уравнении вектор  полностью известен и по величине и по направлению (отрезок
полностью известен и по величине и по направлению (отрезок 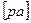 , изображающий этот вектор, уже отложен). Вектор
, изображающий этот вектор, уже отложен). Вектор  направлен перпендикулярно звену
направлен перпендикулярно звену 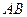 , а вектор
, а вектор 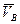 - по направляющей
- по направляющей  . Величины этих векторов неизвестны.
. Величины этих векторов неизвестны.
Согласно векторному уравнению, через конец вектора  (через точку
(через точку 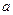 ) проводим направление вектора
) проводим направление вектора  , а через начало вектора
, а через начало вектора  (через полюс
(через полюс 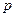 ) – направление вектора
) – направление вектора 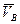 . Точку пересечения указанных направлений обозначим
. Точку пересечения указанных направлений обозначим 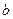 . Тогда отрезки
. Тогда отрезки 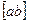 и
и 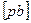 в выбранном масштабе будут соответствовать скоростям последовательно
в выбранном масштабе будут соответствовать скоростям последовательно  и
и 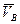 .
.
Измеряем эти отрезки по плану скоростей:
 мм,
мм,  мм;
мм;
вычисляем соответствующие скорости:
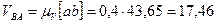 м/с;
м/с;
 м/с.
м/с.
Скорость точки  определяем по теореме подобия
определяем по теореме подобия
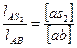 , откуда
, откуда  .
.
По заданию  , тогда
, тогда 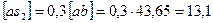 мм,
мм,
где 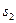 - точка на плане скоростей, соответствующая точке
- точка на плане скоростей, соответствующая точке  механизма.
механизма.
Откладывая отрезок  на плане скоростей, вдоль отрезка
на плане скоростей, вдоль отрезка 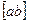 , получим точку
, получим точку 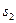 . Соединяя эту точку с полюсом, получим отрезок
. Соединяя эту точку с полюсом, получим отрезок  , изображающий в масштабе вектор
, изображающий в масштабе вектор 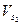 . Измеряем величину этого отрезка
. Измеряем величину этого отрезка  мм
мм
и вычисляем скорость 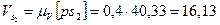 м/с.
м/с.
Определяем угловую скорость шатуна 2:
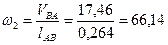 с-1.
с-1.
Для определения направления угловой скорости 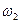 следует вектор
следует вектор  перенести в точку
перенести в точку 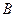 механизма и посмотреть, как она в соответствии с направлением этого вектора движется относительно точки
механизма и посмотреть, как она в соответствии с направлением этого вектора движется относительно точки  . В нашем случае
. В нашем случае 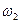 направлена против часовой стрелки.
направлена против часовой стрелки.
Аналогично строим план скоростей для второй группы Ассура (4,5). Составляем векторное уравнение
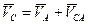
Вектор 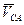 направлен перпендикулярно звену
направлен перпендикулярно звену  , а вектор
, а вектор 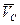 - по направляющей
- по направляющей 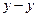 . Величины этих векторов неизвестны.
. Величины этих векторов неизвестны.
Для решения векторного уравнения через конец вектора  (точка
(точка 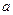 ) проводим направление вектора
) проводим направление вектора  , а через начало вектора
, а через начало вектора  (через полюс
(через полюс 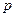 ) – направление вектора
) – направление вектора 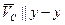 . Точку пересечения направлений обозначим
. Точку пересечения направлений обозначим 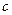 .
.
 м/с;
м/с;
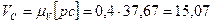 м/с.
м/с.
Скорость точки  определяем по теореме подобия
определяем по теореме подобия
 , откуда
, откуда 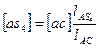 .
.
По заданию 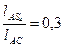 , тогда
, тогда  мм.
мм.
Откладываем отрезок 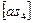 на плане скоростей, вдоль отрезка
на плане скоростей, вдоль отрезка  , получим точку
, получим точку 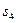 и соединяем ее с полюсом.
и соединяем ее с полюсом.
 м/с.
м/с.
Определяем угловую скорость шатуна 4
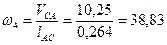 с-1.
с-1.
Для определения направления угловой скорости  переносим вектор
переносим вектор 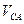 в точку
в точку  механизма и смотрим, как она в соответствии с направлением этого вектора движется относительно точки
механизма и смотрим, как она в соответствии с направлением этого вектора движется относительно точки  . В данном положении механизма
. В данном положении механизма 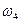 направлена по часовой стрелке.
направлена по часовой стрелке.
Аналогичным образом строим планы скоростей для всех двенадцати положений механизма. Полученные значения скоростей заносим в таблицу скоростей (табл. 2.1).
Построение плана ускорений
План ускорений строится для заданного положения механизма (координата  ).
).
Для механизма первого класса определяем ускорение точки  , совершающей вращательное движение по окружности радиуса
, совершающей вращательное движение по окружности радиуса  . Условно принимаем
. Условно принимаем 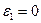 , тогда полное ускорение точки
, тогда полное ускорение точки  равно ее нормальному ускорению
равно ее нормальному ускорению
 м/с2.
м/с2.
Вектор 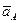 направлен по кривошипу
направлен по кривошипу  от точки
от точки  к точке
к точке  (к центру вращения кривошипа).
(к центру вращения кривошипа).
Задаваясь масштабом плана ускорений  м∙c-2/ мм, определяем величину отрезка
м∙c-2/ мм, определяем величину отрезка 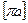 , изображающего вектор
, изображающего вектор 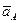 на плане ускорений:
на плане ускорений:
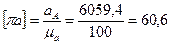 мм.
мм.
Выбираем произвольную точку 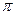 (полюс) и откладываем этот отрезок в указанном направлении.
(полюс) и откладываем этот отрезок в указанном направлении.
Составляем векторное уравнение для определения ускорения точки 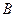 группы Ассура 2-3:
группы Ассура 2-3:
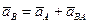 (2.1)
(2.1)
Разложим ускорение 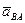 на составляющие
на составляющие
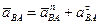 , (2.2)
, (2.2)
тогда
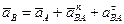 (2.3)
(2.3)
В этом уравнении вектор 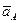 уже полностью известен, а величина вектора
уже полностью известен, а величина вектора  вычисляется по формуле:
вычисляется по формуле:
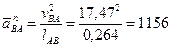 м/с².
м/с².
| Таблица 2.1
| ω4
|
| 38,83
| 66,14
| 75,76
| 66,14
| 38,83
|
| 38,83
| 66,14
| 75,76
| 66,14
| 38,83
|
| ω2
| 75,76
| 66,14
| 38,83
|
| 38,83
| 66,14
| 75,76
| 65,72
| 38,83
|
| 38,83
| 66,14
|
| VS4
| 20,0
| 18,05
| 15,01
| 14,0
| 15,01
| 18,05
| 20,0
| 19,31
| 16,13
| 14,0
| 16,13
| 19,31
|
| ps4
| 50,0
| 45,12
| 37,53
| 35,0
| 37,53
| 45,12
| 50,0
| 48,27
| 40,33
| 35,0
| 40,33
| 48,27
|
| VS2
| 14,0
| 16,13
| 19,31
| 20,0
| 18,05
| 15,01
| 14,0
| 15,28
| 18,05
| 20,0
| 19,31
| 16,13
|
| ps2
| 35,0
| 40,33
| 48,27
| 50,0
| 45,52
| 37,53
| 35,0
| 37,53
| 45,12
| 50,0
| 48,20
| 40,33
|
| VC
| 20,0
| 15,07
| 7,78
|
| 7,78
| 15,07
| 20,0
| 19,57
| 12,22
|
| 12,22
| 19,57
|
| pc
| 50,0
| 37,67
| 19,46
|
| 19,46
| 37,67
| 50,0
| 48,94
| 30,54
|
| 30,54
| 48,94
|
| VB
|
| 12,22
| 19,50
| 20,0
| 15,07
| 7,78
|
| 7,78
| 15,07
| 20,0
| 19,5
| 12,22
|
| pb
|
| 30,54
| 48,94
| 50,0
| 37,67
| 19,46
|
| 19,46
| 37,67
| 50,0
| 48,94
| 30,54
|
| VCA
|
| 10,25
| 17,46
| 20,0
| 17,46
| 10,25
|
| 10,25
| 17,46
| 20,0
| 17,46
| 10,25
|
| ac
|
| 25,63
| 43,65
| 50,0
| 43,65
| 25,63
|
| 25,63
| 43,65
| 50,0
| 43,65
| 25,63
|
| VBA
| 20,0
| 17,46
| 10,25
|
| 10,25
| 17,46
| 20,0
| 17,35
| 10,25
|
| 10,25
| 17,35
|
| ab
| 50,0
| 43,65
| 25,63
|
| 25,63
| 43,65
| 50,0
| 43,36
| 25,63
|
| 25,63
| 43,65
|
| № пол
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим величину отрезка  , изображающего вектор
, изображающего вектор  на плане ускорений,
на плане ускорений,
 мм.
мм.
Векторы в уравнении (2.3) направлены следующим образом:  ,
,  (направлен от точки
(направлен от точки 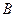 к точке
к точке  ),
),  .
.
В соответствии с правой частью векторного уравнения к вектору 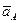 прикладываем вектор
прикладываем вектор  (т.е. от точки
(т.е. от точки 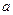 откладываем в указанном направлении отрезок
откладываем в указанном направлении отрезок  , а через конец вектора
, а через конец вектора  (через точку
(через точку  ) проводим направление вектора
) проводим направление вектора  ). В соответствии с левой частью уравнения через полюс
). В соответствии с левой частью уравнения через полюс 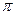 проводим направление вектора
проводим направление вектора  . Точку пересечения указанных направлений обозначим буквой
. Точку пересечения указанных направлений обозначим буквой 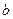 . Таким образом, отрезки
. Таким образом, отрезки  и
и  изображают в масштабе соответственно ускорению
изображают в масштабе соответственно ускорению  и
и  . Измеряем величины этих отрезков и вычисляем ускорения:
. Измеряем величины этих отрезков и вычисляем ускорения:
 м/с2;
м/с2;
 м/с2.
м/с2.
Соединяя точки 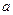 и
и 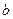 , получим отрезок
, получим отрезок 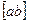 , который в соответствии с уравнением (2.2) изображает вектор полного относительного ускорения
, который в соответствии с уравнением (2.2) изображает вектор полного относительного ускорения 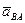 . Измеряем величину этого отрезка и вычисляем ускорение:
. Измеряем величину этого отрезка и вычисляем ускорение:
 м/с2.
м/с2.
Определяем ускорение точки  . По теореме подобия имеем:
. По теореме подобия имеем:
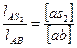 ,
,
(по заданию 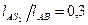 ), тогда
), тогда 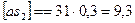 мм.
мм.
Откладывая этот отрезок вдоль отрезка 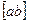 , получим точку
, получим точку 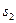 . Соединяя ее с полюсом
. Соединяя ее с полюсом 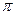 , получим отрезок
, получим отрезок 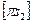 , изображающий вектор
, изображающий вектор 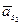 . Измеряем этот отрезок и вычисляем ускорение
. Измеряем этот отрезок и вычисляем ускорение
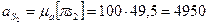 м/с2.
м/с2.
Находим величину углового ускорения шатуна 2
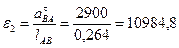 с-2.
с-2.
Для определения направления 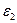 следует вектор
следует вектор  перенести в точку
перенести в точку 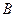 механизма и посмотреть, как она в соответствии с этим вектором движется относительно точки
механизма и посмотреть, как она в соответствии с этим вектором движется относительно точки  . В нашем случае
. В нашем случае 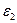 направлено по часовой стрелке.
направлено по часовой стрелке.
Аналогично строим план ускорений для второй группы Аcсура (4-5).
Составляем векторное уравнение:
 (2.4)
(2.4)
Разложив ускорение  на составляющие, получим:
на составляющие, получим:
 (2.5)
(2.5)
В этом уравнении вектор  полностью известен, а величина вектора
полностью известен, а величина вектора  вычисляется по формуле:
вычисляется по формуле:
 м/с2.
м/с2.
Отрезок  , изображающий ускорение
, изображающий ускорение  , на плане ускорений определится:
, на плане ускорений определится:
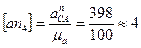 мм.
мм.
Векторы в уравнении (2.5) направлены следующим образом:  ,
,  (направлен от точки
(направлен от точки  к точке
к точке  ),
),  .
.
В соответствии с правой частью векторного уравнения к вектору 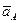 прикладываем вектор
прикладываем вектор  (т.е. от точки
(т.е. от точки 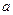 откладываем в указанном направлении отрезок
откладываем в указанном направлении отрезок  , а через конец вектора
, а через конец вектора  (через точку
(через точку 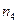 ) проводим направление вектора
) проводим направление вектора  ).
).
В соответствии с левой частью уравнения через полюс 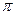 проводим направление вектора
проводим направление вектора 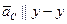 . Точку пересечения указанных направлений обозначим точкой
. Точку пересечения указанных направлений обозначим точкой  . Таким образом, отрезки
. Таким образом, отрезки  и
и 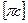 изображают в масштабе соответственно ускорению
изображают в масштабе соответственно ускорению  и
и 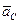 . Измеряем величины этих отрезков и вычисляем ускорения:
. Измеряем величины этих отрезков и вычисляем ускорения:
 м/с2;
м/с2;
 м/с2.
м/с2.
Соединяя точки 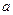 и
и 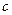 , получим отрезок
, получим отрезок  , который изображает вектор полного относительного ускорения
, который изображает вектор полного относительного ускорения  . Измеряем величину этого отрезка и вычисляем ускорение:
. Измеряем величину этого отрезка и вычисляем ускорение:
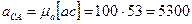 м/с2.
м/с2.
Определяем ускорение точки 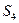 . По теореме подобия имеем:
. По теореме подобия имеем:
 , откуда
, откуда  мм.
мм.
Откладывая этот отрезок вдоль отрезка  , получим точку
, получим точку 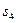 . Соединяя ее с полюсом
. Соединяя ее с полюсом 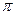 , получим отрезок
, получим отрезок  , изображающий вектор
, изображающий вектор 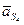 . Измеряем этот отрезок и вычисляем ускорение:
. Измеряем этот отрезок и вычисляем ускорение:
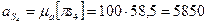 м/с2.
м/с2.
Находим величину углового ускорения шатуна 4:
 с-2.
с-2.
Для определения направления  следует вектор
следует вектор  перенести в точку
перенести в точку  механизма и посмотреть, как она в соответствии с этим вектором движется относительно точки
механизма и посмотреть, как она в соответствии с этим вектором движется относительно точки  . В нашем случае
. В нашем случае  направлено по часовой стрелке.
направлено по часовой стрелке.

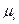 указывает количество единиц изображаемой величины в 1 мм чертежа. При построении планов механизма желательно масштабный коэффициент
указывает количество единиц изображаемой величины в 1 мм чертежа. При построении планов механизма желательно масштабный коэффициент 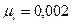 м/мм, тогда отрезок изображающий на чертеже длину
м/мм, тогда отрезок изображающий на чертеже длину  звена
звена  определится:
определится: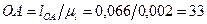 мм.
мм.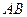 и
и  на чертеже.
на чертеже.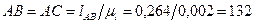 мм.
мм. (ось вращения звена 1) и намечаем траектории точки
(ось вращения звена 1) и намечаем траектории точки 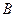 ползуна 3 (
ползуна 3 (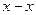 ) и точки
) и точки  ползуна 5 (
ползуна 5 ( ). Далее радиусом
). Далее радиусом  . На этой окружности на одинаковом расстоянии друг от друга (
. На этой окружности на одинаковом расстоянии друг от друга ( ) наносим положение т.
) наносим положение т. 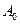 , соответствующую крайнему верхнему положению ползуна
, соответствующую крайнему верхнему положению ползуна  ) выделяется основными линиями, а остальные положения вычерчиваются тонкими линиями.
) выделяется основными линиями, а остальные положения вычерчиваются тонкими линиями. . Модуль скорости точки
. Модуль скорости точки 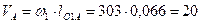 м/с,
м/с,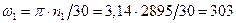 рад/с.
рад/с.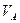 направлен перпендикулярно радиусу кривошипа в сторону его вращения.
направлен перпендикулярно радиусу кривошипа в сторону его вращения.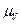 выбираем таким образом, чтобы отрезок
выбираем таким образом, чтобы отрезок  , изображающий скорость
, изображающий скорость 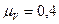 (м×с‾¹)/мм, тогда отрезок
(м×с‾¹)/мм, тогда отрезок  .
. мм.
мм.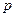 - полюса плана скоростей откладываем в указанном направлении отрезок
- полюса плана скоростей откладываем в указанном направлении отрезок 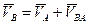 .
. полностью известен и по величине и по направлению (отрезок
полностью известен и по величине и по направлению (отрезок 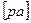 , изображающий этот вектор, уже отложен). Вектор
, изображающий этот вектор, уже отложен). Вектор  направлен перпендикулярно звену
направлен перпендикулярно звену 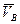 - по направляющей
- по направляющей  . Величины этих векторов неизвестны.
. Величины этих векторов неизвестны.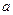 ) проводим направление вектора
) проводим направление вектора 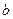 . Тогда отрезки
. Тогда отрезки 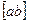 и
и 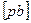 в выбранном масштабе будут соответствовать скоростям последовательно
в выбранном масштабе будут соответствовать скоростям последовательно  мм,
мм,  мм;
мм;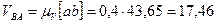 м/с;
м/с; м/с.
м/с. определяем по теореме подобия
определяем по теореме подобия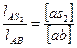 , откуда
, откуда  .
. , тогда
, тогда 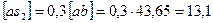 мм,
мм,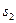 - точка на плане скоростей, соответствующая точке
- точка на плане скоростей, соответствующая точке  на плане скоростей, вдоль отрезка
на плане скоростей, вдоль отрезка  , изображающий в масштабе вектор
, изображающий в масштабе вектор 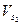 . Измеряем величину этого отрезка
. Измеряем величину этого отрезка  мм
мм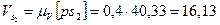 м/с.
м/с.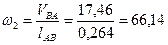 с-1.
с-1.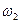 следует вектор
следует вектор  перенести в точку
перенести в точку 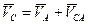
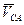 направлен перпендикулярно звену
направлен перпендикулярно звену 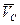 - по направляющей
- по направляющей 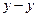 . Величины этих векторов неизвестны.
. Величины этих векторов неизвестны. , а через начало вектора
, а через начало вектора 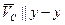 . Точку пересечения направлений обозначим
. Точку пересечения направлений обозначим 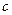 .
. м/с;
м/с;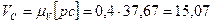 м/с.
м/с. определяем по теореме подобия
определяем по теореме подобия , откуда
, откуда 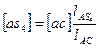 .
.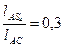 , тогда
, тогда  мм.
мм.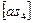 на плане скоростей, вдоль отрезка
на плане скоростей, вдоль отрезка  , получим точку
, получим точку 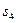 и соединяем ее с полюсом.
и соединяем ее с полюсом. м/с.
м/с.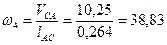 с-1.
с-1. переносим вектор
переносим вектор 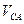 в точку
в точку 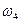 направлена по часовой стрелке.
направлена по часовой стрелке.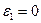 , тогда полное ускорение точки
, тогда полное ускорение точки  м/с2.
м/с2.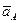 направлен по кривошипу
направлен по кривошипу  м∙c-2/ мм, определяем величину отрезка
м∙c-2/ мм, определяем величину отрезка 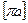 , изображающего вектор
, изображающего вектор 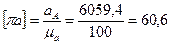 мм.
мм.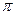 (полюс) и откладываем этот отрезок в указанном направлении.
(полюс) и откладываем этот отрезок в указанном направлении.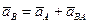 (2.1)
(2.1)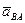 на составляющие
на составляющие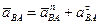 , (2.2)
, (2.2)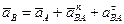 (2.3)
(2.3) вычисляется по формуле:
вычисляется по формуле: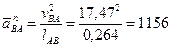 м/с².
м/с². , изображающего вектор
, изображающего вектор  мм.
мм. ,
,  (направлен от точки
(направлен от точки  .
. ) проводим направление вектора
) проводим направление вектора  . Точку пересечения указанных направлений обозначим буквой
. Точку пересечения указанных направлений обозначим буквой  и
и  изображают в масштабе соответственно ускорению
изображают в масштабе соответственно ускорению  и
и  . Измеряем величины этих отрезков и вычисляем ускорения:
. Измеряем величины этих отрезков и вычисляем ускорения: м/с2;
м/с2; м/с2.
м/с2. м/с2.
м/с2. . По теореме подобия имеем:
. По теореме подобия имеем: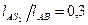 ), тогда
), тогда 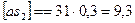 мм.
мм.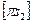 , изображающий вектор
, изображающий вектор 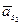 . Измеряем этот отрезок и вычисляем ускорение
. Измеряем этот отрезок и вычисляем ускорение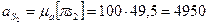 м/с2.
м/с2.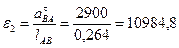 с-2.
с-2.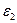 следует вектор
следует вектор  (2.4)
(2.4) на составляющие, получим:
на составляющие, получим: (2.5)
(2.5) полностью известен, а величина вектора
полностью известен, а величина вектора  вычисляется по формуле:
вычисляется по формуле: м/с2.
м/с2. , изображающий ускорение
, изображающий ускорение 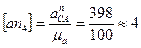 мм.
мм. ,
,  (направлен от точки
(направлен от точки  .
.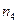 ) проводим направление вектора
) проводим направление вектора 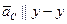 . Точку пересечения указанных направлений обозначим точкой
. Точку пересечения указанных направлений обозначим точкой  и
и 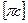 изображают в масштабе соответственно ускорению
изображают в масштабе соответственно ускорению  и
и 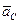 . Измеряем величины этих отрезков и вычисляем ускорения:
. Измеряем величины этих отрезков и вычисляем ускорения: м/с2;
м/с2; м/с2.
м/с2. , который изображает вектор полного относительного ускорения
, который изображает вектор полного относительного ускорения 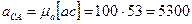 м/с2.
м/с2.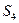 . По теореме подобия имеем:
. По теореме подобия имеем: мм.
мм. , изображающий вектор
, изображающий вектор 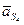 . Измеряем этот отрезок и вычисляем ускорение:
. Измеряем этот отрезок и вычисляем ускорение: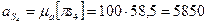 м/с2.
м/с2. с-2.
с-2. следует вектор
следует вектор 


