Решение. 1. Полные сопротивления фаз:1. Полные сопротивления фаз:
2. Фазные (они же линейные) токи:
3. Углы сдвига фаз между фазным током и фазным напряжением в каждой фазе:
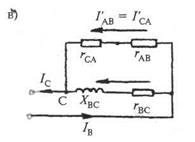
4. Построение векторной диаграммы начинаем с фазных напряжений UА, UB, UС (рис. 4б), располагая их под углом 120° друг относительно друга. Чередование фаз принято обычным: за фазой А — фаза В, за фазой В — фаза С (в положительном направлении). Под углами МU = 55В /см; МI = 10 А/см. Ток в фазе А совпадает с фазным напряжением Пример 5. Для схемы, приведенной на рис.5а, начертить в масштабе векторную диаграмму, из которой графически определить линейные токи. Как изменятся линейные токи при отключении линейного провода А? Начертить для этого случая векторную диаграмму. Линейное напряжение сети U = 220В.
Рис. 5
|
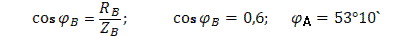
к соответствующим векторам фазных напряжений откладываем векторы линейных токов I А, 1В, 1С к соответствующим векторам фазных напряжений откладываем векторы линейных токов 
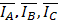. Геометрическая сумма последних равна току в нулевом проводе I0 = 18 А. При построении векторной диаграммы были приняты масштабы:
; ток в фазе В отстает от фазного напряжения UB на угол φB =53°10`; ток в фазе С совпадает с фазным напряжением 
На этой же диаграмме показаны векторы линейных напряжений трическая сумма трех линейных токов дает ток в нулевом проводе I0 = 18 А. При отключении линейного провода А ток I0 = 0, а токи IВ и IC не меняют своей величины. Ток в нулевом проводе в этом случае равен геометрической сумме токов 
(см. построение I0 на рис. 4б). Из диаграммы находим графически I0 = 38 A.
