Введение. При распространении света в среде с резкими неоднородностями наблюдается явление дифракции, то есть нарушение законов геометрической оптики
При распространении света в среде с резкими неоднородностями наблюдается явление дифракции, то есть нарушение законов геометрической оптики, приводящее к отклонению распространения света от прямолинейного вблизи краев непрозрачных тел. Данное явление обусловлено волновой природой света. В случае, когда дифракция наблюдается в сходящихся (непараллельных) лучах, говорят о дифракции Френеля.
Рис. 1 Рассмотрим дифракцию Френеля на примере распространения сферической световой волны через круглое отверстие в непрозрачном экране. Для того, чтобы определить действие световой волны в какой-либо точке Р на линии ОО ' (рис. 1), воспользуемся методом зон Френеля. Разобьем открытую волновую поверхность на кольцевые зоны Френеля, построенные таким образом, чтобы расстояние от краев соседних зон до точки Р отличалось на половину длины волны λ/2.
Рис. 2
Определим площади и радиусы зон Френеля. Согласно рис. 2, имеет место соотношение
где rm – радиус зоны Френеля под номером m; R – радиус волновой поверхности; hm – высота сферического сегмента, выделяемого внешней границей m -й зоны; b – расстояние от волновой поверхности до точки наблюдения P;
Ввиду малости λ при небольших значениях m можно пренебречь слагаемым, содержащим λ2. С учетом этого приближения из формулы (1) следует
Так как площадь сферического сегмента Sm = 2p R
Следовательно, площади зон Френеля примерно одинаковы (Δ Sm не зависит от m). Полагая hm << R, из соотношения (1) получим для радиуса зоны Френеля под номером m выражения rm =2 Rhm, или с учетом (2),
Очевидно, если rm является одновременно радиусом r рассматриваемого отверстия в экране, то оно открывает часть волнового фронта, на котором умещается число зон Френеля, равное
Интенсивность света в точке наблюдения Р зависит от числа m открытых зон Френеля. Колебания, возбуждаемые в точке Р вторичными источниками от аналогичных участков соседних зон, будут находиться в противофазе, то есть ослаблять друг друга (по определению расстояния до указанных участков от точки Р отличаются на λ / 2). Следовательно, если отверстие открывает четное число зон Френеля, в точке Р наблюдается минимум освещенности, нечетное – максимум. Амплитуды колебаний, возбуждаемых зонами в точке Р, в соответствии с принципом Гюйгенса-Френеля образуют монотонно убывающую последовательность
A1 > А2 >... > A m -1 >A m > A m +1 >...
Это связано с тем, что площади зон примерно одинаковы, а расстояния bm от зоны до точки наблюдения Р увеличиваются с ростом m. Кроме того, от центральной зоны к периферическим увеличивается угол j между нормалью к элементам зоны и направлением на точку Р (см. рис. 1). Амплитуда результирующего колебания равна алгебраической сумме амплитуд:
A = A 1- A 1+ A 3- A 4+... (6)
Здесь знак минус учитывает, что фазы колебаний, возбуждаемые соседними зонами, отличаются на p. Преобразуем выражение (6) к виду
Вследствие монотонного убывания Аm можно приближенно считать, что Как следует из соотношения (5), при фиксированных длине волны излучения λ, размерах отверстия r и расстоянии между источником света S и точкой наблюдения Р освещенность в точке Р будет зависеть от положения экрана – расстояний R и b.
|



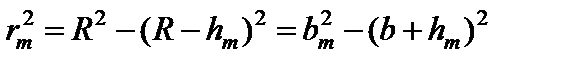 , (1)
, (1) – расстояние от точки P до границы зоны Френеля под номером m.
– расстояние от точки P до границы зоны Френеля под номером m.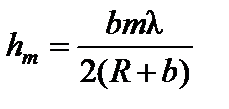 (2)
(2) hm, выражение для площади m -й зоны имеет вид
hm, выражение для площади m -й зоны имеет вид . (3)
. (3)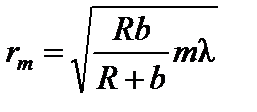 . (4)
. (4) . (5)
. (5) (7)
(7) . Тогда выражения в скобках будут равны нулю, и амплитуда колебания в точке Р, возбуждаемого полностью открытым волновым фронтом, окажется равной А = A 1 / 2. Если отверстие открывает только одну центральную зону Френеля, то амплитуда колебания равна А = А 1, то есть в два раза больше. Соответственно интенсивность I в точке Р (которая пропорциональна квадрату амплитуды) при одной открытой зоне в четыре раза больше, чем при полностью открытом волновом фронте так как I ~ А 2 [2].
. Тогда выражения в скобках будут равны нулю, и амплитуда колебания в точке Р, возбуждаемого полностью открытым волновым фронтом, окажется равной А = A 1 / 2. Если отверстие открывает только одну центральную зону Френеля, то амплитуда колебания равна А = А 1, то есть в два раза больше. Соответственно интенсивность I в точке Р (которая пропорциональна квадрату амплитуды) при одной открытой зоне в четыре раза больше, чем при полностью открытом волновом фронте так как I ~ А 2 [2].


