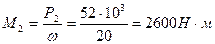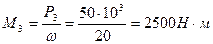Пример выполнения расчетно-графической работы. Для стального вала (рис. 1, а) постоянного по длине сечения требуется: 1) определить значения моментов М2 и М3

Для стального вала (рис. 1, а) постоянного по длине сечения требуется: 1) определить значения моментов М₂ и М₃, соот­ветствующие передаваемым мощностям Р₂ и Р₃, а также уравновешивающий момент М₁; 2) построить эпю­ру крутящих моментов; 3) определить требуемый диаметр вала из расчетов на прочность и жесткость, полагая по ва­рианту (а) поперечное сечение вала — круг; по варианту (б) — поперечное се­чение вала — кольцо, имеющее соотно­шение диаметров с = d_a/d = 0,8.

Принять: [τ_к]=30 МПа; [φ₀] = = 0,02 рад/м = 0,02·10^-3 рад/мм; Р₂=52 кВт;Р₃=50 кВт; ώ = 20 рад/с; G = 8·10⁴ МПа.

Окончательное значение диаметра округлить до ближайшего четного (или оканчивающегося на пять) числа.

Решение. 1. Определяем внешние скручивающие моменты:

2. Определяем уравновешивающий момент М₁:

ΣМ_i=0; М₁-М₂-М₃=0; М₁= М₂+М₃=5100 Нм

3. Определяем крутящий момент по участкам вала:

Мz₁=М₁=5100 Нм;

Мz_II=М₁-М₂=5100-2600=2500 Нм.

 

Строим эпюру крутящих моментов Мz. (рис 1, б)

 

 

Рис. 1

 

4. Определяем диаметр вала из условий прочности и жесткости:

Мz_max = 5100 Нм (рис. 1, б)

 

Требуемый диаметр получился больше из расчета на прочность, поэтому его принимаем как окончательный d= 95 мм.

 

Требуемые диаметры окончательно принимает из расчетов на прочность: d=114 мм; d₀=0,8d=0,8·114=91,2 мм. Принимаем d₀=92 мм.

Расчетно-графическая работа №7

по теме:

«Проектный расчет балки, работающей на изгиб, из условия прочности»

Последовательность решения задачи:

1. Балку разделить на участки по характерным сечениям.

2. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.

 

3. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие мо­менты в характерных сечениях и построить эпюру изгибающих моментов.

 

4. Для данной балки, имеющей по всей длине постоянное попе­речное сечение, выполнить проектный расчет, т. е. определить W_x в опас­ном сечении, где изгибающий момент имеет наибольшее по модулю значение.