Пример выполнения расчетно-графической работы.
Рис. 1
1. Изображаем вал со всеми действующими на него силами, а также оси координат (рис. 1,б). 2. Определяем F2 и Fr2. Из условия равновесия вала, имеющего неподвижную ось:
Σ Mz (Fi)=0;
3. Составляем шесть уравнений равновесия: Σ Mx (Fi)=0; Σ Mx = -RBy Σ My (Fi)=0; Σ My = 3F1 Σ Mx1 (Fi)=0; Σ Mx1 = RAy Σ My1 (Fi)=0; Σ My1 = RAx Σ Xi=0; Σ Xi= 3F1+ Fr2 - RAx - RBx = 0; (5) Σ Yi=0; Σ Yi= RAy – F2 + RBy = 0; (6)
4. Решаем уравнения (1), (2), (3), (4) и определяем реакции опор: из (1) RBy= из (2) RBx= из (3) RAy= из (4) RAx=
5. Проверяем правильность найденных реакций опор. Используем уравнение (5):
Σ Xi = 3F1+ Fr2 - RAx - RBx = 300 + 120 – 264 – 156 = 0
Следовательно, реакции RAx и RBx определены верно. Используем уравнение (6): Σ Yi = RAy – F2 + RBy = 60 – 300 – 240 = 0
Следовательно, реакции RAy и RBy определены верно.
по теме: «Построение эпюр продольных сил, нормальных напряжений и определение деформации бруса при растяжении и сжатии» Последовательность решения задачи:
1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения. 2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N), построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провестилинии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам. 3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т. е. эпюра на данном участке изображается прямой, параллельной оси бруса. 4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
Пример. Для данного ступенчатого бруса (рис. 1, а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е=2*105МПа; F1 = 30KH = 30·103 Н; F2= 38·103 Н;
по теме: «Проектный расчет и оценка прочности стандартного сечения стержня, работающего на растяжение и сжатие» Последовательность решения задачи: 1. Определить реакции стержней, используя уравнения равновесия для плоской системы сходящихся сил и проверить правильность найденных реакций.
2. Для наиболее нагруженного стержня, используя условие прочности [А]≥
3. Определить процент пере- или недогрузки наиболее нагруженного стержня, используя условие прочности σ≤[σ], при принятых
|

 На вал (рис 1,а) жестко насажены шкив 1 и колесо 2. Определить силы F2, Fr2= 0,4 F2, а также реакции опор А и В, если F1= 100 Н.
На вал (рис 1,а) жестко насажены шкив 1 и колесо 2. Определить силы F2, Fr2= 0,4 F2, а также реакции опор А и В, если F1= 100 Н.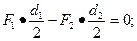
 Fr2= 0,4
Fr2= 0,4  F2= 0,4
F2= 0,4  300= 120 Н
300= 120 Н CB- Fr2
CB- Fr2 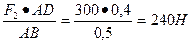 ;
; ;
; ;
;



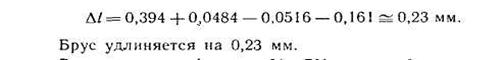


 , определить площадь поперечного сечения стержня, подобрать по сортаменту (ГОСТ 8509—72) подходящий номер профиля и найти стандартное значение площади поперечного сечения стержня.
, определить площадь поперечного сечения стержня, подобрать по сортаменту (ГОСТ 8509—72) подходящий номер профиля и найти стандартное значение площади поперечного сечения стержня.


