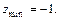Понятие локального экстремума для функции нескольких переменных вводится аналогично тому, как это сделано для функции одной переменной. Например, для функции 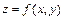 ситуация ясна из рис. 4.18.1: полное приращение D z должно быть знакопостоянным в некоторой проколотой окрестности точки
ситуация ясна из рис. 4.18.1: полное приращение D z должно быть знакопостоянным в некоторой проколотой окрестности точки 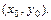 При этом
При этом
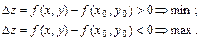
Иногда рассматривают так называемые нестрогие экстремумы:

(рис. 4.18.2). Мы такие точки изучать не будем.
Для нахождения локальных экстремумов воспользуемся формулой Тейлора (положим в ней
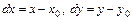
):
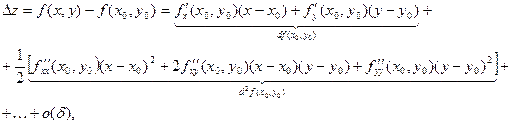
(4.18.1)
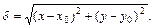
Из формулы (4.18.1) сразу следует, что при  или
или  величина
величина 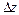 будет содержать хотя бы одну из разностей
будет содержать хотя бы одну из разностей  или
или 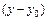 в первой степени. Поскольку при этом
в первой степени. Поскольку при этом  то приращение
то приращение 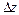 знакопостоянным не будет. Таким образом, имеем необходимые условия экстремума (для дифференцируемой функции):
знакопостоянным не будет. Таким образом, имеем необходимые условия экстремума (для дифференцируемой функции):

 (4.18.2)
(4.18.2)
При выполнении условий (4.18.2) касательная плоскость к поверхности 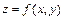 будет параллельна плоскости Оху, а соответствующая точка
будет параллельна плоскости Оху, а соответствующая точка  называется стационарной точкой функции
называется стационарной точкой функции 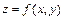 .
.
Пусть выполняются условия (4.18.2), а среди производных второго порядка имеются отличные от нуля в точке  .
.
Тогда согласно (4.18.1)

Выражение в квадратных скобках представляет собой квадратичную форму переменных  и
и 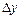 с матрицей
с матрицей
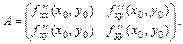 (4.18.3)
(4.18.3)
Для того чтобы в точке  функция имела экстремум, достаточным условием является положительная (максимум) или отрицательная (минимум) определенность квадратичной формы, т.е. собственные значения матрицы (4.18.3) должны быть одного знака. Отсюда, обозначив для краткости
функция имела экстремум, достаточным условием является положительная (максимум) или отрицательная (минимум) определенность квадратичной формы, т.е. собственные значения матрицы (4.18.3) должны быть одного знака. Отсюда, обозначив для краткости
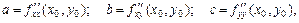
получим
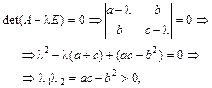
т.е. достаточное условие того, чтобы квадратичная форма была положительно или отрицательно определенной:
 ;
;
или 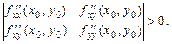
Если  то
то  и
и 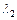 будут иметь различные знаки – это случай минимакса (рис.4.18.3). Квадратичная форма здесь будет знакопеременной, и экстремум отсутствует.
будут иметь различные знаки – это случай минимакса (рис.4.18.3). Квадратичная форма здесь будет знакопеременной, и экстремум отсутствует.
 Если
Если  то одно из чисел
то одно из чисел  равно нулю, и вопрос об экстремуме остается открытым (необходим анализ дифференциалов более высоких порядков).
равно нулю, и вопрос об экстремуме остается открытым (необходим анализ дифференциалов более высоких порядков).
Таким образом, если выполняются условия (4.18.2), (4.18.4), то в точке  функция
функция  имеет экстремум (минимум при
имеет экстремум (минимум при 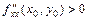 и максимум при
и максимум при  ).
).
Если количество переменных больше двух, т.е. рассматривается функция  , то вопрос в принципе решается аналогично: при выполнении
, то вопрос в принципе решается аналогично: при выполнении
условий
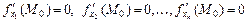
квадратичная форма, отвечающая дифференциалу
 ,
,
должна быть положительно или отрицательно определенной, т.е. все  должны иметь один и тот же знак. Однако при этом столь простого условия, как (4.18.4), не получается.
должны иметь один и тот же знак. Однако при этом столь простого условия, как (4.18.4), не получается.
П р и м е р
Исследовать на локальный экстремум функцию 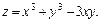
Решение: 1. Вычислим  и найдем стационарные точки функции из системы
и найдем стационарные точки функции из системы
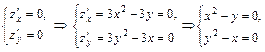
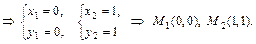
2. Вычислим  и составим
и составим
 .
.
В точке  имеем
имеем  Поэтому
Поэтому  не является точкой экстремума. В точке
не является точкой экстремума. В точке  имеем
имеем 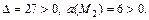 Поэтому
Поэтому  является точкой минимума, причём
является точкой минимума, причём 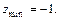
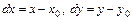 ):
):

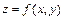 ситуация ясна из рис. 4.18.1: полное приращение D z должно быть знакопостоянным в некоторой проколотой окрестности точки
ситуация ясна из рис. 4.18.1: полное приращение D z должно быть знакопостоянным в некоторой проколотой окрестности точки 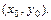 При этом
При этом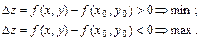



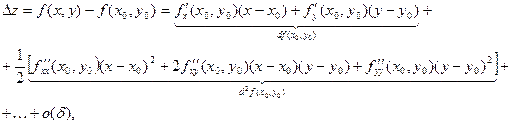
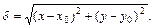
 или
или  величина
величина 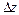 будет содержать хотя бы одну из разностей
будет содержать хотя бы одну из разностей  или
или 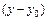 в первой степени. Поскольку при этом
в первой степени. Поскольку при этом  то приращение
то приращение 
 (4.18.2)
(4.18.2) называется стационарной точкой функции
называется стационарной точкой функции 
 и
и 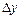 с матрицей
с матрицей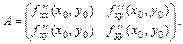 (4.18.3)
(4.18.3)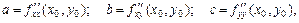
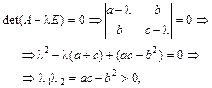
 ;
;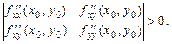
 то
то  и
и 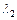 будут иметь различные знаки – это случай минимакса (рис.4.18.3). Квадратичная форма здесь будет знакопеременной, и экстремум отсутствует.
будут иметь различные знаки – это случай минимакса (рис.4.18.3). Квадратичная форма здесь будет знакопеременной, и экстремум отсутствует. Если
Если  то одно из чисел
то одно из чисел  равно нулю, и вопрос об экстремуме остается открытым (необходим анализ дифференциалов более высоких порядков).
равно нулю, и вопрос об экстремуме остается открытым (необходим анализ дифференциалов более высоких порядков). имеет экстремум (минимум при
имеет экстремум (минимум при 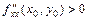 и максимум при
и максимум при  ).
). , то вопрос в принципе решается аналогично: при выполнении
, то вопрос в принципе решается аналогично: при выполнении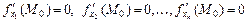
 ,
,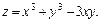
 и найдем стационарные точки функции из системы
и найдем стационарные точки функции из системы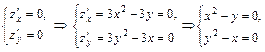
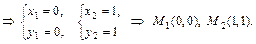
 и составим
и составим .
. имеем
имеем  Поэтому
Поэтому  имеем
имеем 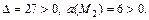 Поэтому
Поэтому