Потери энергии в установившихся режимах работы электропривода.
Полученное в параграфе 2,1 соотношение (12) относилось к статическому установившемуся режиму работы нерегулируемого привода. В регулируемых приводах наряду с выбором способа регулирования скорости или момента необходимо учитывать потери в преобразовательных устройствах с целью обеспечения экономичности привода. А) При регулировании скорости электропривода постоянные потери, состоящие из потерь в цепи возбуждения, механических, потерь в стали и преобразователях, в целом будут изменяться. Однако, потери на возбуждение и в преобразователях остаются практически постоянными (если отсутствует изменение магнитного потока), а потери в стали и механические можно считать изменяемыми пропорционально квадрату скорости. Б) Переменные потери вращающегося преобразователя определяются аналогично таковым для двигателей. К переменным потерям статического преобразователя относятся потери в меди силового трансформатора и в вентилях. При частотном регулировании скорости машин переменного тока составляющая постоянных потерь – потери в стали статора - существенным образом зависит от диапазона регулирования частоты. Поскольку рабочее скольжение остается небольшим на всем диапазоне изменения скоростей, остальные виды постоянных потерь остаются примерно постоянными. А как же обстоит дело с переменными потерями, определяемыми выражением: v = 3I При частотном регулировании скорости, за счет постоянства момента двигателя, перепад скорости Δω = ω
2.3 Потери энергии в переходных процессах и способы их уменьшения.
Известно, что в переходных процессах ток двигателя, а соответственно и переменные потери значительно превышают номинальные. В этом случае постоянными потерями, как правило, можно пренебречь. Суммарные потери энергии в переходных режимах определяются выражением: ΔW = В общем случае они оказываются сложной функцией, зависящей от нагрузки на валу, от механической и электромагнитной инерционности двигателя и т.п. Чтобы лучше понять физическую сторону возникновения потерь в переходных режимах электропривода будем пренебрегать электромагнитной инерционностью двигателя и постоянными потерями. Рассматривать будем только активные потери, имеющие место в рабочих цепях двигателей и преобразователей. В соответствии со сделанными допущениями и с допускаемым равенством 3I ΔW = где t s = Δω / ω А) Сначала упростим задачу и найдем выражение для потерь при отсутствии нагрузки, при этом потери энергии будут обусловлены только переходным процессом. Подставим в (20) выражение для момента из уравнения движения при М ΔW Из приведенного выражения видно, что производная потерь энергии (подинтегральная функция) по скорости не зависит от времени и равна разности количеств движений при скорости ω Проинтегрировав выражение (21), получим формулу для определения потерь (переменных) при изменении скорости от ω ω ΔW = J ω Заменяя значение скоростей ω ΔW Таким образом, при изменении скорости затрачивается количество энергии, равное разности кинетических энергий при начальной и конечной скоростях привода, выраженных через запас кинетической энергии привода при скорости ω Какими же будут потери энергии в приводе при различных случаях переходных процессов? Рассмотрим некоторые из них, подставляя в (22) или (23) соответствующие начальные условия. а) Процесс пуска: ω При этом ΔW
|

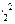 (R
(R 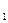 + R
+ R  ) = Mω
) = Mω  s(1 +
s(1 +  ) (18)
) (18) ΔP dt =
ΔP dt =  = Mω
= Mω 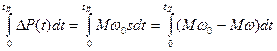 , (20)
, (20) - время переходного процесса;
- время переходного процесса; = 0, т.е. М = J
= 0, т.е. М = J  dω/dt, и получим:
dω/dt, и получим: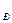 =
= 
 . (21)
. (21) до ω
до ω  вхолостую:
вхолостую: - J
- J  ω
ω  /2
/2  (22)
(22) (s
(s  -s
-s  )/2. (23)
)/2. (23)


