Двигатели постоянного тока с независимым возбуждением

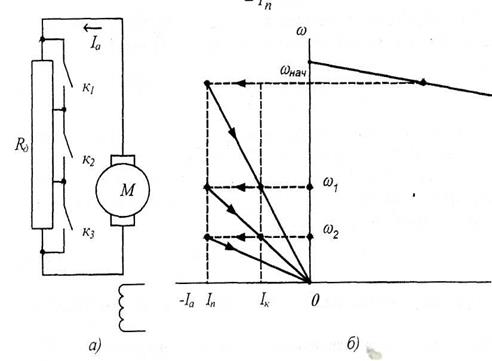
Для управления работой двигателя производятся необходимые изменения параметров и воздействий, определяющих положение его механических характеристик. В соответствии с (3.5) такими параметрами и воздействиями являются приложенное к якорной цепи напряжение U_c, суммарное сопротивление якорной цепи R_яц, и магнитный поток машины Ф. Характеристики, соответствующие измененным параметрам двигателя или специальным схемам его включения, принято называть искусственными механическими характеристиками.

1. Изменение напряжения, подведенного к якорной обмотке двигателя при номинальном потоке, является в регулируемом ЭП постоянного тока основным управляющим воздействием. Как правило, изменение напряжение U_я возможно только в сторону уменьшения по сравнению с номинальным, причем для мощных двигателей это ограничение является жестким, так как допустимое по условиям работы коллектора повышение напряжения невелико и опасно.

Как следует из (3.5), при изменении U_я пропорционально изменяется скорость идеального холостого хода двигателя, а жесткость механических характеристик при любом напряжении одинакова, поэтому механические характеристики при U_я=var имеют вид параллельных прямых, показанных на рис. 3.2. Изменение напряжения на якоре позволяет не только изменять скорость вращения, но и ограничивать ток короткого замыкания. Плавное повышение напряжения питания

двигателя от 0 до U_ном обеспечивает наиболее благоприятные условия пуска двигателя.

Рисунок 3.2 – Механические характеристики двигателя с независимым

возбуждением при U_я = var.

2. Искусственные характеристики, полученные путем введения добавочных резисторов в цепь якоря, называются реостатными характеристиками. Схема включения резисторов (сопротивлений) для получения реостатных характеристик представлена на рис. 3.3,а. При этом суммарное сопротивление якорной цепи увеличивается:

R_яΣ = R_{я дв} + R_доб.

Ток короткого замыкания ограничивается величиной I_к.з.= U_ном/(R_{я дв} + R_доб), а модуль жесткости механической характеристики уменьшается:

β = k²Ф_ном² /(R_{я дв}+ R_доб) = с² / R_яΣ.

Скорость идеального холостого хода остается неизменной и равной ω_0ном, а между током и моментом двигателя, если не учитывать реакцию якоря, сохраняется пропорциональность М = кФ_ном I_я.

Семейство реостатных механических характеристик представлено на рис.3.3,б.

Введение резисторов в цепь якоря двигателя является простейшим средством ограничения тока при различных переходных процессах и используется для этих целей во всех случаях при питании двигателя от сети.

Снижение жесткости механических характеристик заставляет уменьшать диапазон допустимого изменения момента нагрузки при одинаковом изменении скорости вращения. Введение резисторов приводит к увеличению потерь энергии в сопротивлениях на тепло.

При питании двигателя от неуправляемого источника питания часто возникает необходимость использовать искусственные характеристики, например для ограничения бросков тока при пуске. С этой цельюв цепь якоря машины включают дополнительные сопротивления (рис.3.3).

Механические характеристики при последовательном шунтировании добавочных сопротивлений приведены на рис.3.4.

При расчете пусковых характеристик прежде всего необходимо определить пусковой момент М_п или соответствующий ему пусковой ток, а также момент переключения М_к, учитывая, что для устойчивого пуска необходимо М_к>М_с.

Рисунок 3.3 - Схема (а) и реостатные характеристики двигателя (б).

М_к – момент, соответствующий переключениям ступеней сопротивлений;

М_п – пусковой момент.

Рисунок 3.4 – Пусковая диаграмма двигателя.

Для выбора М_п необходимо сравнить величину допустимого момента по условиям механической прочности электромеханической системы и допустимую величину тока (момента) двигателя (приводится в справочниках) При заданном числе ступеней М_к. выбирается таким образом, чтобы на всех ступенях обеспечить постоянство М_к и М_п. При выборе числа ступеней следует учитывать, что с увеличением числа ступеней с одной стороны увеличивается количество пуско-регулирующей аппаратуры, а с другой, - увеличивается средний за время пуска динамический момент, что приводит к уменьшению времени пуска.Поскольку настройка аппаратуры выполняется по величине токов, то расчеты удобнее выполнять по электромеханической характеристике двигателя и уравнению равновесия напряжений (3.2), предварительно определив I_п = М_п / kФ_н и I_к = М_к / kФ_н. Тогда полное сопротивление цепи якоря на первой ступени будет: R_Σ = U_я / I_п, где R_Σ=R_я + r₁ + r₂ + r₃. Шунтирование первой ступени сопротивления r₁ должно происходить при скорости ω₁ и токе I_к. Тогда из (3.2) получим:

R₁ = (U_я - kФ_нω₁) / I_п, (3.6)

где R₁ = R_я = r₂ + r₃.

Сопротивления, остающиеся в цепи якоря после шунтирования остальных секций, определяются таким же образом:

R₂ = U_я - kФ_нω₂ / I_п R₃ = U_я - kФ_нω₃ / I_п (3.7)

Зная r_я нетрудно вычислить сопротивления каждой секции. При расчете механических характеристик необходимо знать величину кФ_н, которая в справочниках не приводится. Эту величину просто рассчитать по уравнению (3.5) в точке номинального режима:

кФ_н = (U_ян - r_яI_ян) / ω_н (3.8)

При торможении двигатель переходит в генераторный режим, преобразуя запасенную кинетическую энергию W = J_Σω²/ 2 в электрическую. Однако для создания тормозного момента эту энергию необходимо вывести из ЭМС. В электроприводах с регулируемым преобразователем электрической энергии, обладающим двухсторонней энергопроводимостью, эта энергия возвращается в источник питания, т.е. обеспечивается торможение с рекуперацией энергии. Если применение более сложного реверсивного преобразователя нецелесообразно, то эта энергия преобразуется в тепловую и рассеивается в окружающую среду. В системах с нерегулируемым источником питания двигателя отдача энергии через тепловую энергию является единственным способом.

Имеются еще два способа торможения: динамическое и торможение противовключением.

а) При динамическом торможении цепь якоря двигателя отключается от источника питания и замыкается на сопротивление R _д (рис. 3.5,а), которое может быть секционировано. В этом случае построение диаграмм и расчет сопротивлений секций выполняется как и при пуске, но с учетом что U_я = 0 и I_я < 0:

R_i = - kФ_н ω_i / - I_п = kФ_н ω_i / I_п (3.9)

б) Противовключением называют режим, при котором якорь двигателя вращается под действием моментов, определяемых запасом кинетической или потенциальной энергии, в противоположном направлении, по сравнению с действием электромагнитного момента.

При наличии реактивного статического момента торможение противовключением получают изменяя полярность напряжения на зажимах якоря, как при реверсе (рисю3.6,а) и включив в цепь якоря тормозной резистор R_пр. После переключения полярности якорь двигателя переходит из начальной точки работы 1 в точку 2 на новой механической характеристике, проходящей через точку ω₀ (рис3.6,б). Благодаря изменению полярности напряжения в сети питания, ток двигателя изменяет свой знак и при работе привода во втором квандранте определяется уравнением I = - (U + E) / R, где R = r_я + R_пр.

При этом происходит интенсивное торможение привода благодаря действию суммарного отрицательного динамического момента

М_дин = - (kФ_нI + M_c) < 0. (3.10)

В точке 3 происходит остановка двигателя, поскольку реактивный статический момент, меняя свой знак, препятствует вращению привода в противоположную сторону.

Если режим торможения противовключением осуществляется с меньшим сопротивлением R_пр, и новая механическая характеристика является лучом, проходящим через точку 4, то тормозной режим противовключения не заканчивается в точке 5. Двигатель может совершить реверс и перейти в двигательный режим работы с установившейся скоростью ω_с, определяемой координатами точки 6. Для исключения реверса привода при достижении им точки 5 на механической характеристике двигатель отключают от сети и осуществляют при необходимости механическое торможение до полной остановки.

Рисунок 3.5 – Схема включения (а) и диаграмма динамического торможения (б).

Рисунок 3.6 – Схема включения (а) и механические характеристики (б) двигателя в режиме торможения противовключеснием при наличии реактивного момента.

При наличии активного статического момента нагрузки режим торможения противовключением получают без переключения полярности напряжения на зажимах якорной обмотки, а лишь введением большого добавочного сопротивления R_пр (рис.3.7,а).

Рисунок 3.7 – Схема включения (а) и механические характеристики двигателя

при наличии активного статического момента (б).

Тогда под действием потенциальных сил (силы тяжести) якорь двигателя затормаживается, а затем начинает вращаться в противоположном напрвлении, и ЭДС меняет свой знак. Поэтому ток (момент) двигателя при работе его в четвертом квадранте, сохраняя прежнее направление, определяется по формуле:

I = [U – (-E)] / R = (U + E) / R.

Процесс перехода из двигательного режима в тормозной (противовключение) изображен на рис.3.7,б. В этом случае оказывается возможным обеспечить тормозной режим с различными скоростями ω_с< 0 и полную остановку привода (точка 6), что зависит от сопротивления R_пр.

Работа привода при скорости - ω_с, применяемая в подъемно-транспортных механизмах, называется силовым спуском груза.

Заметим, что при идентичных исходных состояния привода, определяемых точкой! и сопротивлением R_пр, процесс достижения нулевой скорости при наличии реактивного момента (точка 3 на рис.3.6,б) будет происходить значительно быстрее, чем при наличии активного момента (точка 3 на рис.3.7,б). Это объясняется тем, что при работе привода в первом квадранте динамический момент, а следовательно, и замедление определяются суммой моментов (3.10), а их разностью: М_дин = (М–М_с) < 0 (3.11)

В отличие от генераторного торможения с отдачей энергии в сеть, в режиме торможения противовключением к двигателю подводится от сети энергия с мощностью Р_эл и со стороны механизма - Р_м. Следовательно, потери ∆p будут:

Таким образом, режим противовключения обеспечивает интенсивное торможение привода до полной остановки, но сопровождается значительным потреблением энергии от сети и существенным нагревом обмоток двигателя и сопротивлений при ее рассеивании.

При расчете добавочных сопротивлений при противовключении на тормозном участке (до реверса) приложенное напряжение и ЭДС двигателя однонаправлены:

R_i = U_z + kФ_н ω_i / I_п. (3.13)

3) Изменение потока двигателя Ф в связи с насыщением его магнитной цепи в номинальном режиме практически возможно только в сторону его уменьшения – ослабления поля двигателя. Согласно (3.4) и (3.5) уменьшение потока вызывает увеличение скорости идеального холостого хода ω₀ и уменьшение момента короткого замыкания М_кз, а ток короткого замыкания при этом не изменяется. Из-за квадратичной зависимости модуля жесткости от магнитного потока изменение механических характеристик происходит как показано на рис.(3.8).

Рис. 3.8 - Электромеханические (а) и механические (б) характеристики двигателя с независимым возбуждением при ослаблении поля

При рассмотрении этих характеристик следует иметь ввиду, что рабочий участок характеристик двигателя ограничивается его перегрузочной способностью и, как показано на рис.3.8 утолщенными отрезками характеристик, лежит вблизи скорости идеального холостого хода. Нетрудно видеть, что ослабление поля в пределах рабочих нагрузок приводит к увеличению скорости двигателя и снижению пускового момента М_п = М_кз.

Основным достоинством такого способа регулирования скорости является его энергетическая экономичность, а недостатком – невозможность обеспечить пуск двигателя. В связи с этим основное применение такого регулирования – изменение скорости в диапазоне выше номинальной.

Рассмотренные выше характеристики двигателя получены в предположении, что он питается от бесконечно мощной сети или от любого другого источника, обладающего свойствами источника напряжения с внутренним сопротивлением, равным нулю. Приступая к изучению динамических свойств, необходимо иметь в виду, что в регулируемом электроприводе возможно питание якорной цепи двигателя и от преобразователей, обладающих свойствами источника тока. Анализ динамических свойств электромеханического преобразователя с независимым возбуждением проведем для случая питания его от источника напряжения.

Для анализа воспользуемся системой исходных уравнений, записанных в операторной форме: ; (3.14)

где Т_В = L_В / R_В – электромагнитная постоянная времени обмотки возбуждения;

Т_Я = L_ЯΣ / R_ЯΣ – электромагнитная постоянная времени якорной цепи;

k_В = Ф/i_В – коэффициент, соответствующий линейной части кривой намагничивания двигателя.

Структурная схема электромеханического преобразователя энергии, соответствующая (3.14), приведена на рис.3.9,а. На схеме представлены два возможных канала управления при питании от источника напряжения – канал управления полем двигателя, которому соответствует управляющее воздействие u_в, и канал управления по цепи якоря с управляющим воздействием u_я.

Рис. 3.9. Структурные схемы электромеханического преобразователя с независимым

возбуждением

Из схемы следует, что при отсутствии реакции якоря процессы в цепи возбуждения протекают независимо от процессов в якорной цепи, а процессы в якорной цепи зависят от изменений магнитного потока двигателя Ф.

Цепь возбуждения двигателя представляет собой апериодическое звено с постоянной времени Т_В. Индуктивность L_В обмотки возбуждения может быть определена по формуле

L_В = 2p_nk_насw_вФ_ном / I_{в ном},

где k_нас =I_{в ном} / I_{в лин} – коэффициент насыщения;

I_{в лин} - ток возбуждения, создающий номинальный поток Ф_ном при

отсутствии насыщения магнитной цепи.

Значение индуктивности L_В, определяемое данной формулой, соответствует линейной части кривой намагничивания. При работе в насыщенной части кривой намагничивания индуктивность и постоянная времени цепи возбуждения уменьшаются тем больше, чем выше насыщение. При отсутствии добавочных сопротивлений у двигателей мощностью от 1 до нескольких тысяч киловатт постоянная времени цепи возбуждения лежит в пределах Т_В = 0,2 – 5 с, причем с увеличением мощности двигателя она быстро возрастает.

При питании от источника напряжения двигатель с независимым возбуждением работает преимущественно при постоянном потоке Ф = Ф_ном = const, при этом уравнение механической характеристики двигателя в соответствии с (3.5) принимает вид

(1 + Т_я р) М = β(ω₀ – ω). (3.15)

Этому уравнению соответствует структурная схема преобразователя, представленная на рис. 3.11,б. Она свидетельствует о том, что при Ф = const электромеханический преобразователь представляет собой апериодическое звено с постоянной времени Т_Я. Индуктивность якорной цепи двигателя может быть вычислена по приближенной формуле

L_ЯΣ ≈ γ U_ном /p_nω_номI_ном, (3.16)

где γ = 0.6 для некомпенсированных и γ = 0.25 для компенсированных двигателей.

Постоянная времени якорной цепи двигателей средней и большой мощности лежит в пределах Т_Я = 0,02 – 0,1с, причем наибольшие значения соответствуют некомпенсированным либо тихоходным двигателям большой мощности.

Суждение о жесткости естественной механической характеристики по статической зависимости М = f(ω) и по модулю статической жесткости β дает правильные представления только для статических режимов или при достаточно плавных изменениях нагрузки. При изменениях нагрузки скачком, а также в установившихся колебательных режимах динамическая характеристика может существенно отклоняться от статической, и необходимо оценивать эти отклонения с помощью частотных характеристик.

При питании якоря двигателя от источника тока i_я = I_Я1 = const при любых изменениях ЭДС двигателя. Система (3.14) при этом приводится к следующему уравнению механической характеристики

(1 + Т_В р) М = u_вk_ф I_Я1 / R_В.

Этому уравнению соответствует структура электромеханического преобразователя, представленная на рис. 3.9,в. Сравнивая рис.3.9, б и в, можно установить, что в режиме питания якоря от источника тока двигатель с независимым возбуждением утрачивает рассмотренные выше электромеханические свойства. Отсутствие зависимости тока якоря от скорости исключает проявление электромеханической связи, и статическая механическая характеристика двигателя при u_в = const, обладает жесткостью, равной нулю.

Как объект управления электромеханический преобразователь при этом представляет собой апериодическое звено с большой постоянной времени Т_В, управляющим воздействием является напряжение, приложенное к обмотке возбуждения u_в. В соответствии с рис.3.9,в электромеханический преобразователь при I_я = const является источником момента М = const, значения которого можно регулировать путем воздействия на инерционный канал возбуждения двигателя.