Колебания.
Любой периодический, повторяющийся во времени процесс называется колебаниями. Колебания имеют различную природу, но их математическое описание одинаково. Это позволяет пользоваться простейшими и наглядными моделями – математическим и пружинным маятниками – и проводить аналогию с механическими колебательными системами в других, менее очевидных ситуациях. Самый простой случай колебаний – это свободные, незатухающие гармонические колебания. Условия для их возникновения следующие: · Однократное воздействие внешней силы, задающее начальные условия. Затем система должна быть предоставлена самой себе. · Наличие в системе только консервативных сил. Очевидно, что в природе это условие не выполняется. · Наличие обратной связи. Возвращающая сила должна быть все время направлена в сторону устойчивого положения равновесия. · Отклонения системы от положения равновесия должны быть достаточно малы. В случае соблюдения указанных условий колеблющаяся величина (например, координата тела) описывается простейшей гармонической функцией:
где каждый параметр имеет свое название: х – смещение, А – амплитуда (максимальное смещение),
j0 = j (t = 0) – начальная фаза (определяется начальными условиями), w0 - собственная круговая (циклическая) частота колебаний, зависящая от свойств самой системы. Размерность w0= рад/с или 1/с. Фазу колебаний можно записать и по-другому:
Здесь Т – период колебаний, показывающий, за какое время совершается одно полное колебание, а n = 1/Т – частота, показывающая, сколько колебаний совершается за единицу времени. [ Т ] = с, [ n ] = 1/с = Гц.
|

 или
или  ,
,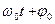 = j - фаза (от греческого “фазис” – состояние), имеет размерность угла “радиан”, т.е. безразмерна, изменяется от j0 до ¥ и определяет состояние системы,
= j - фаза (от греческого “фазис” – состояние), имеет размерность угла “радиан”, т.е. безразмерна, изменяется от j0 до ¥ и определяет состояние системы, .
.


