Свободные гармонические затухающие колебания и вынужденные колебания.
В реальных системах всегда имеются неконсервативные силы. Поэтому закон сохранения механической энергии в них не выполняется; говорят, что имеет место диссипация энергии, а сами системы называют диссипативными. В таких системах амплитуда колебаний будет постепенно уменьшаться, и колебания в конце концов прекратятся (затухнут). Полная повторяемость процессов в диссипативных системах отсутствует, но можно говорить о частичной, приблизительной повторяемости, и такие процессы также относят к классу колебаний. Учет неконсервативных сил, т.е. сопротивления, приводит к следующей зависимости смещения от времени:
где b – коэффициент затухания, который определяется сопротивлением, а частота График зависимости смещения от времени для затухающих колебаний выглядит следующим образом: Амплитуда убывает тем быстрее, чем больше сопротивление Чтобы компенсировать потери энергии в колебательной системе, в технических устройствах используют работу периодически действующей силы F = F0 cos (Wt). Эта внешняя по отношению к системе сила после того, как собственные колебания системы вследствие диссипации затухнут, вынуждает ее колебаться с частотой W. Поэтому силу называют вынуждающей, а сами колебания – вынужденными. Амплитуда вынужденных колебаний зависит и от свойств самой системы, и от величины сопротивления, и от частоты вынуждающей силы W: А = А(w0,b,W). Можно показать, что при определенных соотношениях между этими параметрами произойдет резкое возрастание амплитуды. Это явление носит название резонанс и может играть как позитивную, так и негативную роль в различных ситуациях. Кроме упомянутых, в физике рассматриваются также параметрические и автоколебания. Колебания, распространяемые автоволнами (см. п.7 данной лекции), называются автоколебаниями. Для их возникновения требуется, чтобы в системе существовала обратная связь. Амплитуда, фаза и частота автоколебаний, в отличие от свободных и вынужденных колебаний, зависит только от свойств системы и не зависят от начальных условий. В фазовом пространстве они представляют собой замкнутую траекторию, к которой стремятся все соседние траектории – так называемый устойчивый предельный цикл. Пример автоколебаний – движение маятника часов.
|

 ,
,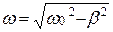 отличается от собственной частоты w0. Видно, что движение будет периодическим только при w0 > b (при достаточно малом сопротивлении).
отличается от собственной частоты w0. Видно, что движение будет периодическим только при w0 > b (при достаточно малом сопротивлении). .
.


