Исследование формы эллипса по его уравнению
Пусть дан эллипс своим каноническим уравнением (4) Для определения вида кривой заданной уравнением (4), заметим: а) Координаты начала системы координат точки О(0;0) не удовлетворяют уравнению (4). => Эллипс не проходит через начало координат. б) Найдём точки пересечения эллипса с осью Ох: в) Найдём точки пересечения эллипса с осью Оу: г) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М1(-х;у) принадлежит эллипсу. => Эллипс симметричен относительно оси Ох. д) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М2(х;-у) принадлежит эллипсу. => Эллипс симметричен относительно оси Оу. На основании г) и д) можно сделать вывод, что эллипс симметричен относительно начала системы координат. е) Из уравнения (4) ж) Так как до з)
Рис.2 Точки А1, А2, В1, В2 ─ называют вершинами эллипса. [A1A2] ─ большой осью эллипса, [B1B2] ─ называют малой осью эллипса. Числа
|
.
=> 
=> Эллипс две точки пересечения с осью Ох: 
и 
.
=> 
=> Эллипс две точки пересечения с осью Ох: 
и 
.
, 
=> 
и 
=> Все точки эллипса лежат внутри прямоугольника, ограниченного прямыми 
, то можно сделать вывод, что с ростом у от 0
величина х убывает от 
до 0.
=> 
=> 
=>
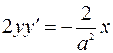<0 => Если 
, то 
, то есть функция 
выпукла вверх. Учитывая симметричность эллипса относительно осей координат, получаем изображение эллипса (Рис.2.).
называют полуосями эллипса.
