Эксцентриситет эллипса
Рассмотрим эллипс с фокусами в точках F1 и F2 , большой полуосью которого является [A1A2]. Определение. Эксцентриситетом эллипса называется число, равное Так как Пусть эллипс задан уравнением
Рис.3. При ε = 0 получаем эллипс является окружностью. При стремлении ε к единице отношение полуосей становится меньше и стремится к нулю. Зафиксируем значение ВЫВОД. Эксцентриситет характеризует степень вытянутости эллипса вдоль большой оси. Параметрические уравнения эллипса Построим на плоскости две окружности с центрами в начале координат и радиусами
Рис.4. Через точку N1 Проведём прямую ℓ1|| (Оу), а через точку N2 ─ прямую ℓ2|| (Ох). Пусть М(х;у) = ℓ1 ∩ ℓ2. Обозначим через α =
Разделив первое равенство системы (6) на
Соотношения (6) называют параметрическими уравнениями эллипса.
|

 .
. , то ε > 0. Для окружности
, то ε > 0. Для окружности 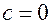 => ε = 0.
=> ε = 0. , тогда
, тогда  => =>
=> =>  =>
=>  . => Эксцентриситет определяется отношением полуосей эллипса.
. => Эксцентриситет определяется отношением полуосей эллипса.
 , что указывает на то, что в этом случае
, что указывает на то, что в этом случае большой полуоси эллипса и пусть ε → 0. Изменение формы эллипса, в этом случае показано на Рис.3.
большой полуоси эллипса и пусть ε → 0. Изменение формы эллипса, в этом случае показано на Рис.3. . Проведём луч из начала координат, и пусть он пересечёт первую окружность в точке N1, а вторую ─ в точке N2. (Рис.4.)
. Проведём луч из начала координат, и пусть он пересечёт первую окружность в точке N1, а вторую ─ в точке N2. (Рис.4.)
 А1ОN1, тогда
А1ОN1, тогда (6)
(6)


