Решение задач
Задача №1. Составить каноническое уравнение эллипса расстояние между фокусами, которого равно 16, а большая ось ─ равна 20. Решение. Если расстояние между фокусами равно 16, то Следовательно, уравнение эллипса имеет вид
Задача №2. Составить уравнение эллипса, если эксцентриситет равен ¾ и эллипс проходит через точку А(1;1). Решение. Для записи канонического уравнения эллипса необходимо знать значения его большой Так как С другой стороны точка А(1;1) принадлежит эллипсу
Так как Запишем каноническое уравнение эллипса
Задача №3. Найти длину перпендикуляра, восстановленного из фокуса эллипса
Восстановим из фокуса F перпендикуляр до пересечения с эллипсом в точке М. По условию задачи необходимо найти длину [FM]. Координаты фокуса F(с;0) определяются по формуле Для нахождения координат точки М необходимо решить систему уравнений
=> Задача №4. Составить каноническое уравнение гиперболы, если её действительная ось равна 2 и расстояние между фокусами равно Решение. Уравнение гиперболы имеет вид Таким образом, уравнение гиперболы имеет вид Задача №5. Составить каноническое уравнение гиперболы, если её эксцентриситет равен 13/5 и гипербола проходит через точку Решение. Для составления канонического уравнения гиперболы необходимо знать значения её действительной По условию задачи дано значение
Уравнение гиперболы имеет вид Задача №6. Составить каноническое уравнение эллипса, если его фокусы совпадают с вершинами гиперболы Решение.
Так как вершины эллипса совпадают с фокусами гиперболы, то Задача №7. На параболе Решение. Каноническое уравнение параболы имеет вид параметр. Уравнение директрисы в общем случае записывается следующим образом Задача №8. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси (Оу) и отсекающей на прямой у = х хорду длины Решение. Пусть парабола имеет уравнение │М1М2│= │2рх│ = Задача №9. Парабола Решение. Пусть парабола имеет уравнение => Задача №10. На параболе Решение. Если точка М(х;у) лежит на параболе Из формулы расстояния от точки до прямой на плоскости следует б) Литература 1. Атанасян Л.С, Базырев В.Т. Геометрия. В 2-х частях. Ч 1 Учебное пособие для студентов физико-математических факультетов пединститутов – М.: Просвещение, 1986.-336 с. 2. Атанасян Л.С., Цаленко М.М. Задачник практикум по геометрии. М.: Просвещение, 1994. – 192 с. 3. Базылев В.Т. и др. Геометрия. Учебное пособие для студентов 1 курса физико-математических факультетов пединститутов М.: Просвещение, 1974. 4. Сборник задач по геометрии/ С.А. Франгулов, П.Н. Совертков, А.А. Фадеева, Т.П. Ходот – М.: Просвещение, 2002 – 238 с.
|

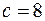 и так как большая ось равна 20, то
и так как большая ось равна 20, то  . Для того чтобы составить уравнение эллипса необходимо определить значение его малой полуоси
. Для того чтобы составить уравнение эллипса необходимо определить значение его малой полуоси  . Воспользуемся следующим соотношением
. Воспользуемся следующим соотношением  =>
=>  = > b = 6.
= > b = 6. .
. и малой
и малой  , то
, то 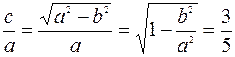
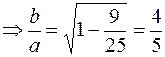 .
.
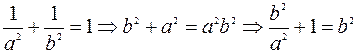 . =>
. => 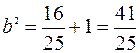 .
. , то
, то 
 .
. .
. Решение.
Решение. . => Прямая (FM) имеет уравнение: х = 4.
. => Прямая (FM) имеет уравнение: х = 4. =>
=> 
 . Очевидно, что │FM│=
. Очевидно, что │FM│= 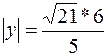 .
. .
. . По условию задачи дано
. По условию задачи дано 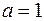 и
и  . Известно, что
. Известно, что  .
.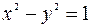 .
. .
.
 . С другой стороны так как точка М принадлежит гиперболе, то её координаты удовлетворяют уравнению:
. С другой стороны так как точка М принадлежит гиперболе, то её координаты удовлетворяют уравнению:  . Таким образом для нахождения значений параметров
. Таким образом для нахождения значений параметров  =>
=> 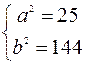 .
.

 , а вершины совпадают с фокусами этой гиперболы.
, а вершины совпадают с фокусами этой гиперболы.
 . С другой стороны фокусы эллипса совпадают с вершинами гиперболы =>
. С другой стороны фокусы эллипса совпадают с вершинами гиперболы => 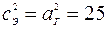 . Так как для эллипса
. Так как для эллипса  , то
, то  . Таким образом уравнение эллипса имеет вид
. Таким образом уравнение эллипса имеет вид  .
. найти точку, расстояние от которой до директрисы равно 4.
найти точку, расстояние от которой до директрисы равно 4.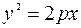 , где р ─
, где р ─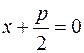 . По условию задачи р = 4 и, следовательно уравнение директрисы х + 2 = 0. Если точка М принадлежит параболе, ео она имеет следующие координаты М(х;
. По условию задачи р = 4 и, следовательно уравнение директрисы х + 2 = 0. Если точка М принадлежит параболе, ео она имеет следующие координаты М(х;  ). Так как расстояние от точки М до директрисы равно 4, то по формуле расстояния от точки до прямой для определения значения х, получаем уравнение:
). Так как расстояние от точки М до директрисы равно 4, то по формуле расстояния от точки до прямой для определения значения х, получаем уравнение:  . Из уравнения параболы следует, что х > 0, поэтому
. Из уравнения параболы следует, что х > 0, поэтому 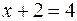 => х = 2 => М(2;
=> х = 2 => М(2;  ).
). .
.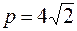 . Искомое уравнение параболы имеет вид
. Искомое уравнение параболы имеет вид  .
.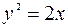
 Написать уравнение этой прямой.
Написать уравнение этой прямой. она имеет две точки пересечения: М1(0;0) и
она имеет две точки пересечения: М1(0;0) и 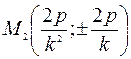 . Длина хорды, очевидно равна
. Длина хорды, очевидно равна 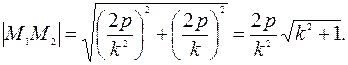 Так как, по условию задачи р = 1 и длина хорды равна 3/4, то для определения параметра
Так как, по условию задачи р = 1 и длина хорды равна 3/4, то для определения параметра  получаем уравнение
получаем уравнение  =>
=> 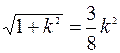 =>
=>  =>
=>  =>
=> Таким образом существуют две прямые
Таким образом существуют две прямые  и
и  , от которых парабола
, от которых парабола 
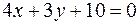 равно 2.
равно 2.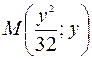 .
.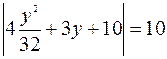 . => а)
. => а)  =>
=>  . Таким образом точки М1(0;0) и М2(18;-24) параболы удалены от прямой
. Таким образом точки М1(0;0) и М2(18;-24) параболы удалены от прямой 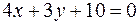 на расстояние, равное 2.
на расстояние, равное 2.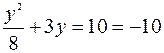 ─ это уравнение не имеет действительных корней.
─ это уравнение не имеет действительных корней.




