Воспользовавшись двенадцатью парами значений (Xt,Yt), t = 1,2,3,…,12 оценили уравнение регрессии
 7,863 + 1,022*Xt,
7,863 + 1,022*Xt,
где  - оценки коэффициентов регрессии, случайные величины, для которых ранее вычислены оценки стандартного отклонения:
- оценки коэффициентов регрессии, случайные величины, для которых ранее вычислены оценки стандартного отклонения:  Поэтому и сама регрессия
Поэтому и сама регрессия  , как сумма случайных величин есть величина случайная. С другой стороны у нас нет другого инструмента для предсказания, кроме как это уравнение регрессии. Пусть за пределами 12-ти пар значений (Xt,Yt) в нашем распоряжении имеется еще одна пара (Х13,Y13). Такую пару легко взять из листа «Задание» файла «Парная регрессия 1» в папке «ЛабРаб». Все исходные данные в вертикальных столбцах листа «Задание» (варианты В-4, В-7, В-10) моделируются по одним и тем же параметрам. Пусть это будут значения из таблицы с индексами Xp и Yp, и будем считать, что Yp нам недоступно. Тогда единственная в нашем случае возможность оценить значение Yp остается предсказать
, как сумма случайных величин есть величина случайная. С другой стороны у нас нет другого инструмента для предсказания, кроме как это уравнение регрессии. Пусть за пределами 12-ти пар значений (Xt,Yt) в нашем распоряжении имеется еще одна пара (Х13,Y13). Такую пару легко взять из листа «Задание» файла «Парная регрессия 1» в папке «ЛабРаб». Все исходные данные в вертикальных столбцах листа «Задание» (варианты В-4, В-7, В-10) моделируются по одним и тем же параметрам. Пусть это будут значения из таблицы с индексами Xp и Yp, и будем считать, что Yp нам недоступно. Тогда единственная в нашем случае возможность оценить значение Yp остается предсказать
его через уравнение регрессии, подставив в него значение Xp = 3,38. Точечная оценка  = 11,32. В данном случае ошибка предсказания равна
= 11,32. В данном случае ошибка предсказания равна 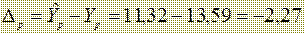 и хотелось бы уяснить, является ли она допустимой с точки зрения точности использованной нами модели. Другое дело, устроит ли эта точность заказчика – лицо, принимающее решение. Но нам следует убедиться пока лишь в том, что эта ошибка укладывается в рамки статистической точности, гарантированной методом наименьших квадратов. Для этого оценим числовые характеристики ошибки. Убедимся, что математическое ожидание ошибки имеет нулевое значение.
и хотелось бы уяснить, является ли она допустимой с точки зрения точности использованной нами модели. Другое дело, устроит ли эта точность заказчика – лицо, принимающее решение. Но нам следует убедиться пока лишь в том, что эта ошибка укладывается в рамки статистической точности, гарантированной методом наименьших квадратов. Для этого оценим числовые характеристики ошибки. Убедимся, что математическое ожидание ошибки имеет нулевое значение.

Дисперсия ошибки прогноза запишется в следующем виде:


Так как  и эта случайная величина состоит из суммы двух случайных величин:
и эта случайная величина состоит из суммы двух случайных величин:  и
и  , умноженной на константу
, умноженной на константу  , то ее дисперсия
, то ее дисперсия  равняется сумме дисперсий
равняется сумме дисперсий  и дисперсии
и дисперсии  , умноженной на квадрат константы
, умноженной на квадрат константы  . Оценки этих дисперсий известны [1]:
. Оценки этих дисперсий известны [1]:  и
и  . Тогда дисперсия
. Тогда дисперсия  оценивается следующей формулой:
оценивается следующей формулой: 
Дисперсия  и ее оценка
и ее оценка 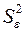 определена выше. Оценка дисперсии прогноза определяется формулой:
определена выше. Оценка дисперсии прогноза определяется формулой:
 (2)
(2)

Рис.37
Формулу (2) можно преобразовать к виду, более удобному для расчета среднеквадратичного отклонения прогноза 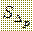 . Из обеих частей формулы (2) извлечем квадратный корень:
. Из обеих частей формулы (2) извлечем квадратный корень:




 . Обозначим
. Обозначим  .
.
Тогда 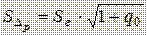
Оценим дисперсию ошибки прогноза исходя из полученных ранее оценок:
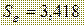 , n = 12, Xp = 3,38., среднее значение Х, вычисленное с помощью функции СРЗНАЧ, равно
, n = 12, Xp = 3,38., среднее значение Х, вычисленное с помощью функции СРЗНАЧ, равно  .,
.,  .
.
Результаты оценки выполнены в Excel и представлены на рис. 37.
Исходные данные для задачи.
Данные о годовом располагаемом доходе и годовых расходах на личное потребление (в 1999 г., в условных единицах) 20 семей. Эти данные представлены в таблице 1.
Табл. 1.
Литература.
1. Бывшев В.А. Введение в эконометрию. Часть 2.-М.: ФА при Правительстве РФ, 2003.

 7,863 + 1,022*Xt,
7,863 + 1,022*Xt, - оценки коэффициентов регрессии, случайные величины, для которых ранее вычислены оценки стандартного отклонения:
- оценки коэффициентов регрессии, случайные величины, для которых ранее вычислены оценки стандартного отклонения:  Поэтому и сама регрессия
Поэтому и сама регрессия  , как сумма случайных величин есть величина случайная. С другой стороны у нас нет другого инструмента для предсказания, кроме как это уравнение регрессии. Пусть за пределами 12-ти пар значений (Xt,Yt) в нашем распоряжении имеется еще одна пара (Х13,Y13). Такую пару легко взять из листа «Задание» файла «Парная регрессия 1» в папке «ЛабРаб». Все исходные данные в вертикальных столбцах листа «Задание» (варианты В-4, В-7, В-10) моделируются по одним и тем же параметрам. Пусть это будут значения из таблицы с индексами Xp и Yp, и будем считать, что Yp нам недоступно. Тогда единственная в нашем случае возможность оценить значение Yp остается предсказать
, как сумма случайных величин есть величина случайная. С другой стороны у нас нет другого инструмента для предсказания, кроме как это уравнение регрессии. Пусть за пределами 12-ти пар значений (Xt,Yt) в нашем распоряжении имеется еще одна пара (Х13,Y13). Такую пару легко взять из листа «Задание» файла «Парная регрессия 1» в папке «ЛабРаб». Все исходные данные в вертикальных столбцах листа «Задание» (варианты В-4, В-7, В-10) моделируются по одним и тем же параметрам. Пусть это будут значения из таблицы с индексами Xp и Yp, и будем считать, что Yp нам недоступно. Тогда единственная в нашем случае возможность оценить значение Yp остается предсказать = 11,32. В данном случае ошибка предсказания равна
= 11,32. В данном случае ошибка предсказания равна 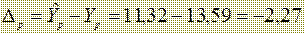 и хотелось бы уяснить, является ли она допустимой с точки зрения точности использованной нами модели. Другое дело, устроит ли эта точность заказчика – лицо, принимающее решение. Но нам следует убедиться пока лишь в том, что эта ошибка укладывается в рамки статистической точности, гарантированной методом наименьших квадратов. Для этого оценим числовые характеристики ошибки. Убедимся, что математическое ожидание ошибки имеет нулевое значение.
и хотелось бы уяснить, является ли она допустимой с точки зрения точности использованной нами модели. Другое дело, устроит ли эта точность заказчика – лицо, принимающее решение. Но нам следует убедиться пока лишь в том, что эта ошибка укладывается в рамки статистической точности, гарантированной методом наименьших квадратов. Для этого оценим числовые характеристики ошибки. Убедимся, что математическое ожидание ошибки имеет нулевое значение.


 и эта случайная величина состоит из суммы двух случайных величин:
и эта случайная величина состоит из суммы двух случайных величин:  и
и  , умноженной на константу
, умноженной на константу  , то ее дисперсия
, то ее дисперсия  равняется сумме дисперсий
равняется сумме дисперсий  и дисперсии
и дисперсии  , умноженной на квадрат константы
, умноженной на квадрат константы  . Оценки этих дисперсий известны [1]:
. Оценки этих дисперсий известны [1]:  и
и  . Тогда дисперсия
. Тогда дисперсия  оценивается следующей формулой:
оценивается следующей формулой: 
 и ее оценка
и ее оценка 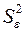 определена выше. Оценка дисперсии прогноза определяется формулой:
определена выше. Оценка дисперсии прогноза определяется формулой: (2)
(2)
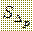 . Из обеих частей формулы (2) извлечем квадратный корень:
. Из обеих частей формулы (2) извлечем квадратный корень:

 . Обозначим
. Обозначим  .
.
 , n = 12, Xp = 3,38., среднее значение Х, вычисленное с помощью функции СРЗНАЧ, равно
, n = 12, Xp = 3,38., среднее значение Х, вычисленное с помощью функции СРЗНАЧ, равно  .,
.,  .
.


