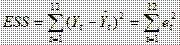Рассмотрим полученный график подробнее.
Представим себе, что нам известны только выборочные значения величины Yt и ее среднее значение. Соответствующая ситуация описывается графиком на рис. 27. В этом
случае разброс значений величины Yt относительно ее среднего значения Представим себе ситуацию, когда известна регрессия
Как видно из этого графика разброс значений
Наконец представим себе вариант, когда известна регрессия
Разброс синих точек относительно регрессии определяется значениями оценок случайной величины et и составляет необъясненную сумму квадратов отклонений, обозначаемую ESS.
В [1] показано, что между этими величинами существует следующая связь:
Напомним, что коэффициент детерминации есть отношение объясненной суммы квадратов отклонений RSS к общей сумме TSS, и чем большая часть суммы квадратов отклонений от среднего объясняется регрессией, тем ближе к 1 значение R2. Аналогично формируется и F-статистика:
|
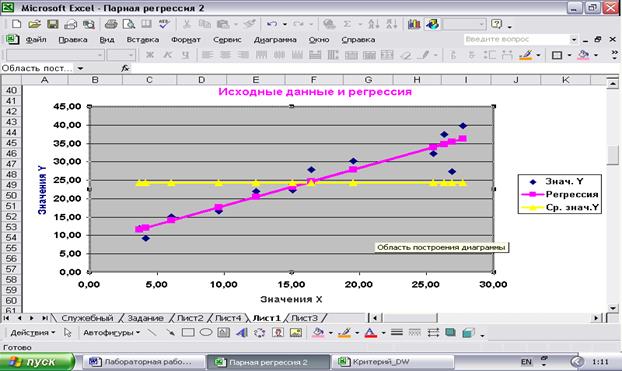Рис.26
Рис.27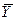
характеризуется суммой квадратов отклонений, которая обозначается TSS [1]. 
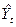и среднее значение 
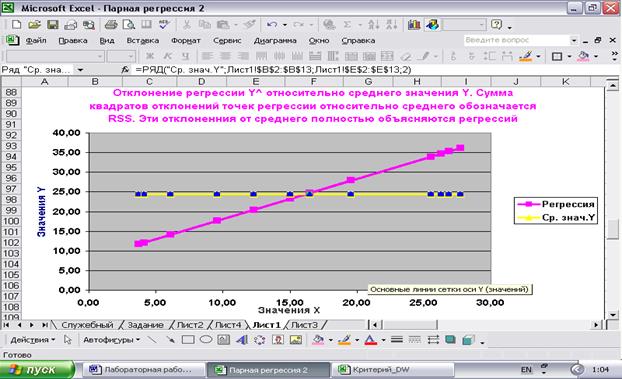Рис.28
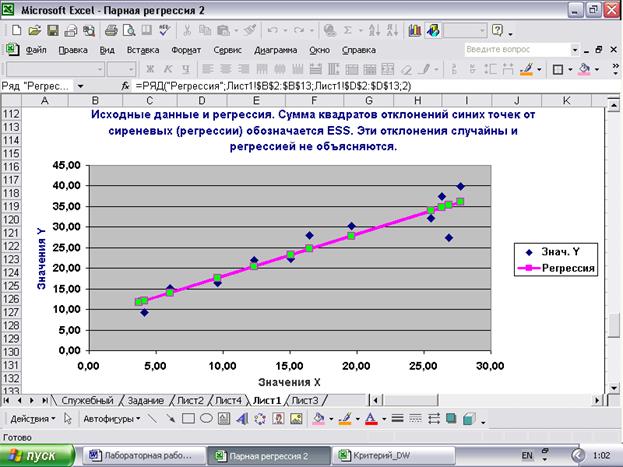Рис.29
