Цель работы. Методом наименьших квадратов оценить коэффициенты линейной регрессии и провести проверку выполнения условий теоремы Гаусса-Маркова.
1. Оформить титульный лист с указанием номера группы, специальности, ФИО исполнителя и номера варианта. 2. Переписать исходные данные из табл. 4 для своего варианта. 3. Представить исходные данные в графическом виде, как это показано на рис. 2 и определить примерный характер аппроксимирующей линейной функции (см. рис. 3 – 6) с оценкой знаков при искомых коэффициентах. 4. Рассчитать коэффициенты уравнения линейной регрессии по формулам (15) и (16). 5. Убедиться в том, что знаки и значения коэффициентов найдены верно по выражению (16а). 6. Представить линейную зависимость на том же графике, где ранее отображены эмпирические данные. 7. Определить прогноз на следующий месяц по общему виду (6), как это сделано в выражении (21). 8. Отобразить значение прогноза на том же графике, как это показано на рис. 2. 7. Рассчитать относительную ошибку аппроксимации по выражению (22). 8. Найти степень тесноты связи (коэффициент линейной корреляции между аргументом и функцией) по выражению (23) и сделать выводы о степени тесноты связи («слабая», «существенная» «сильная», «практически отсутствует»). Проверить нулевую гипотезу о несвязанности х и у, для чего: 9. Рассчитать значение параметра Стьюдента по формуле (24). 10. Определить значение степеней свободы по выражению (26). 11. Выбрать в табл. 4 пороговые табличные значения параметра Стьюдента для вероятностей 90, 95 и 99 процентов. 10. Осуществить сравнение рассчитанного и табличных параметров Стьюдента по нестрогому неравенству (25). 11. Сделать вывод о степени принятия или непринятия нулевой гипотезы о взаимосвязи функции и аргумента. 12. Сформулировать общий вывод по сделанной работе.
Выполненная и оформленная контрольная работа должна быть представлена в учебную часть вуза до начала очередной сессии.
Варианты контрольной работы по дисциплине «Статистика»
Предлагаются варианты, где в течение семи месяцев оценивается прибыль малого предприятия (в десятках тыс. руб.). Требуется составить прогноз на прибыль на следующий, восьмой месяц и сделать необходимые выводы.
Таблица 5 Варианты контрольной работы
Лабораторная работа № 1 «Парная регрессия» Цель работы. Методом наименьших квадратов оценить коэффициенты линейной регрессии и провести проверку выполнения условий теоремы Гаусса-Маркова.
Основная спецификация математической модели имеет вид:
Условия теоремы накладывают ограничения на случайную компоненту Математическое ожидание Ковариация соседних значений Дисперсия случайной компоненты D( Если эти условия выполняются, то оценки неизвестных коэффициентов Сам метод наименьших квадратов (МНК) и вычислительные формулы для расчета оценок коэффициентов приводятся в учебном пособии [1]. Здесь же следует пояснить следующее. Исходными для вычисления коэффициентов регрессии являются табличные значения пар чисел {(X1,Y1), (X2,Y2),…,(Xn,Yn). Из формулы (1) видно, что в ее правой части стоит случайная величина
|


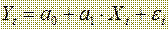 (1)
(1)
 неизвестные коэффициенты регрессии, подлежащие оценке;
неизвестные коэффициенты регрессии, подлежащие оценке;  последовательность случайных величин, удовлетворяющих условиям теоремы Гаусса-Маркова, t = 1,2,…n.
последовательность случайных величин, удовлетворяющих условиям теоремы Гаусса-Маркова, t = 1,2,…n.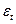 и заключаются они в следующем:
и заключаются они в следующем: при
при  равна 0 -
равна 0 -  .
.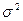 = const.
= const. оказываются несмещенными (т.е. М(
оказываются несмещенными (т.е. М( ) =
) =  и М(
и М( ) =
) =  ), эффективными (имеющих наименьшую дисперсию в классе всех линейных несмещенных оценок) и состоятельными (при большой выборке пар значений (Xt, Yt) D(
), эффективными (имеющих наименьшую дисперсию в классе всех линейных несмещенных оценок) и состоятельными (при большой выборке пар значений (Xt, Yt) D(


