Оценивание коэффициентов регрессии. Функция ЛИНЕЙН.

Табличный редактор EXCEL содержит добротный набор встроенных функций, облегчающих и ускоряющих процесс решения задач эконометрики. Приступая к лабораторной работе необходимо скопировать в свой файл таблицу исходных данных в соответствии с вариантом, заданным преподавателем. Исходные данные содержатся на листе «Исходные данные» файла «Парная регрессия 1» в папке «ЛабРаб».

Рис.1

Вариант В-1 и его размещение в окне процессора EXCEL приведен на рис. 1. Для статистических расчетов оценок коэффициентов регрессии и статистик, оценивающих результаты этих расчетов, воспользуемся функцией ЛИНЕЙН. Но прежде чем обратиться к этой функции необходимо подготовить место на листе EXCEL для вывода результатов расчета. При этом используется следующее правило:

Количество строк всегда равно 5;

количество столбцов равно числу k+1, где k равно числу независимых (экзогенных) переменных.

В случае парной регрессии k=1 и число столбцов равно 2.

Для поиска функции ЛИНЕЙН необходимо выполнить одно из следующих действий:

нажать клавиши <Shift>-<F3>;;

Задать команду ФУНКЦИЯ из меню ВСТАВКА;

нажать кнопку [fx] на стандартной панели.

В ответ на это действие появится диалоговое окно выбора типа функции:

Рис.2

В окне «Категория» щелкнем левой клавишей мышки, в результате чего окно раскроется:

Рис.3

В раскрывшемся окне выделим категорию функций «Статистические» и прокруткой справа найдем в окне «Выберите функцию» функцию ЛИНЕЙН:

Рис.4

Щелкнув мышкой на клавише «ОК» получим следующий результат:

Рис.5

На этом рисунке слева вверху виднеется часть таблицы Вашего варианта расчета, ниже занимает почти всю площадь окна диалоговое окно, все 4 окошечка которого предстоит заполнить, а справа в ячейках (J3:K7) располагается выделенное ранее место для регистрации результата расчетов. Окно «Аргументы функции» легко смещается с помощью мышки в пределах окна монитора, позволяя заполнять 2 верхних окошка y и x координатами соответствующих массивов из таблицы исходных данных. В окошечки «Конст» и «Статистика» как правило заносятся единицы, что соответствует требованию рассчитывать оценки обоих коэффициентов регрессии (в случае, если в окошке «Конст» занесен “0” оценивается только один коэффициент ) и вывести все результаты расчета в ячейки (J3:K7).Заполненное окно показано на рис. 6 ниже.

Рис.6

Далее нажимаем с помощью мышки клавишу «ОК» и большое окно приобретает вид:

Рис.7

Видно, что вычисления не заполняют выделенную справа таблицу - заполнена только одна ячейка с адресом J3. Чтобы заполнить эту таблицу полностью необходимо подвести курсор мышки в строку, где записана функция ЛИНЕЙН(С2:С13;В2:В13;1;1) и щелкнуть левой клавишей мышки. Окно EXCEL приобретет вид:

Рис.8

Теперь необходимо нажать одновременно клавиши <Ctrl>-<Shift>-<Enter> и результаты расчета заполнят таблицу справа полностью:

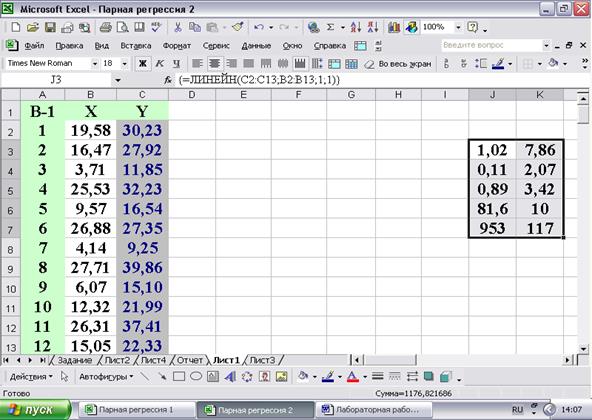
Рис.9

Рассмотрим подробнее информацию, полученную в результате обработки исходных данных функцией ЛИНЕЙН (рис.10).

Рис.10

Первая строка дает оценки коэффициентов регрессии и в соответствии с формулой (1) результат расчетов может быть записан так:

Yt = 7,863 + 1,022*Xt + εt,

где t = 1,2,…,12.

Вторая строка несет информацию о разбросе случайных величин и . Среднеквадратичное отклонение составляет: = 2,074 и = 0,113. В третьей строке справа указана оценка среднеквадратичного отклонения случайной составляющей εt и она равна = 3,418. Оценка дисперсии равна: =3,4182 =11,68. Поскольку процесс моделировался с параметрами , = 1, = 10, то можно утверждать, что получены неплохие оценки для такой выборки (n=12).

В третьей строке слева подсчитан коэффициент детерминации: R2 = 0,891. Это хорошее значение для коэффициента R2, который характеризует качество подгонки регрессии к значениям Yt. Наилучший вариант при R2 = 1 возник бы в том случае, если бы все значения Yt лежали на прямой . Наихудший случай характеризуется значением R2 = 0. Он возникает в том случае, когда уравнение регрессии описывается одной константой , которая в этом случае просто совпадает с . По определению . Проверка значимости коэффициента R2 производится путем сравнения значения F-статистики, значение которой приводится в четвертой строке слева и равно 81,56, с критическим значением Fкр, определяемого функцией EXCEL FРАСПОБР из категории «Статистические».Для обращения к этой функции необходимо: