На рис. 11,а к звеньям приложена известная сила  , которую мы уже нашли из решения предыдущей структурной группы, и реакции отброшенных связей:
, которую мы уже нашли из решения предыдущей структурной группы, и реакции отброшенных связей: 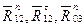 и
и  . Нормальная составляющая реакции направлена вдоль звеньев, а тангенциальная – перпендикулярно соответствующим звеньям.
. Нормальная составляющая реакции направлена вдоль звеньев, а тангенциальная – перпендикулярно соответствующим звеньям.
Запишем векторное уравнение сил для этой структурной группы
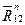 +
+  +
+  +
+  +
+  = 0;
= 0;
В этом уравнении полностью известна реакция  , а все остальные известны только по направлению. Таким образом, имеются четыре неизвестных, две из которых – тангенциальные составляющие
, а все остальные известны только по направлению. Таким образом, имеются четыре неизвестных, две из которых – тангенциальные составляющие  и
и  - найдем аналитически из условия равенства нулю суммы моментов всех сил относительно внутренней кинематической пары C отдельно для каждого из звеньев, а две – нормальные составляющие
- найдем аналитически из условия равенства нулю суммы моментов всех сил относительно внутренней кинематической пары C отдельно для каждого из звеньев, а две – нормальные составляющие 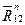 и
и  – из плана сил. Итак:
– из плана сил. Итак:
для 2-го звена:  .
. 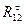 ∙ВС=0; =>
∙ВС=0; => 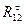 =0.
=0.
для 3-го звена:  .
.  ∙СD-
∙СD-  ∙
∙  =0; =>
=0; =>  .
.
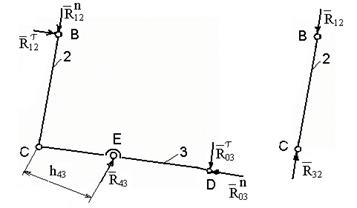
а б
Рис. 11. Расчетная схема для структурной группы звеньев 2-3 (а)
и звена 2 (б)

Теперь строим план сил (рис. 12). Сначала чертим друг за другом в выбранном масштабе сил известные вектора  и
и  . Затем через конец вектора
. Затем через конец вектора  проводим направление нормальной составляющей
проводим направление нормальной составляющей  , а через начало вектора
, а через начало вектора  направление нормальной составляющей
направление нормальной составляющей 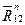 . Точка пересечения этих направлений ограничивает соответствующие реакции. Стрелки ставим так, чтобы вектора шли один за другим.
. Точка пересечения этих направлений ограничивает соответствующие реакции. Стрелки ставим так, чтобы вектора шли один за другим.
Вектор 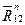 одновременно является и полной реакцией
одновременно является и полной реакцией  , так как
, так как 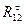 =0. По масштабу сил найдем числовое значение реакций.
=0. По масштабу сил найдем числовое значение реакций.
Для нахождения реакции во внутренней кинематической паре необходимо рассмотреть равновесие одного из звеньев группы. В данном случае проще рассмотреть равновесие второго звена (рис. 11,б): в точке В приложена реакция  , и для равновесия звена в точке С необходимо приложить
, и для равновесия звена в точке С необходимо приложить  .
.
Таким образом, найдены реакции во всех кинематических парах этой группы и можно перейти к ведущему звену.

 , которую мы уже нашли из решения предыдущей структурной группы, и реакции отброшенных связей:
, которую мы уже нашли из решения предыдущей структурной группы, и реакции отброшенных связей: 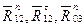 и
и  . Нормальная составляющая реакции направлена вдоль звеньев, а тангенциальная – перпендикулярно соответствующим звеньям.
. Нормальная составляющая реакции направлена вдоль звеньев, а тангенциальная – перпендикулярно соответствующим звеньям.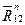 +
+  +
+  +
+  +
+  = 0;
= 0; .
. 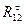 ∙ВС=0; =>
∙ВС=0; =>  ∙СD-
∙СD-  ∙
∙  =0; =>
=0; =>  .
.

 , так как
, так как  .
.


