Структурная группа звеньев 4-5
Рисуем эту группу в любом масштабе длин, прикладываем внешние силы и реакции связей (рис. 18). Сила тяжести и сила инерции ползуна лежат на одной вертикали, но направлены в разные стороны. Поэтому их можно изобразить одним вектором ( Для определения реакций используем условия равновесия структурной группы: векторная сумма всех сил должна быть равна нулю и сумма моментов этих сил тоже должна быть равна нулю. Запишем первое условие:
В этом уравнении три неизвестные величины реакций. Одну - Итак, Σ МF = 0; R 34τ× EF – G 4× hG 4 = 0 Þ R 34τ = G 4
а б
Рис. 18. Расчетная схема структурной группы звеньев 4-5: а – для группы; б – для пятого звена
Теперь можно строить план сил для этой структурной группы (рис. 19, а). Откладываем в любом удобном масштабе сил µ р =[Н/мм] последовательно известные силы
а) б)
Рис. 19. План сил для структурной группы (а) и пятого звена (б)
Из рис. 19, а видно, что на расчетной схеме направление реакций указано правильно. Если начало вектора Таким образом, мы нашли реакции во внешних кинематических парах группы: F – поступательной и Е – вращательной. Теперь найдем реакцию во внутренней кинематической паре F вращательной, соединяющей звенья 4 и 5. Для этого нужно рассмотреть равновесие любого из звеньев группы. Обычно рассматривают то звено, к которому приложено меньше сил. У нас это звено 5. Рисуем расчетную схему рис. 18,б и кроме известных сил Можно заметить, что если при построении плана сил структурной группы последовательно откладывались силы, приложенные к одному звену, а затем силы, приложенные к другому, то на этом же плане сил можно показать реакцию во внутренней кинематической паре. На рис. 19, а реакция
|

 )*. Кроме того, на ползун 5 со стороны отброшенной стойки-направляющей действует реакция
)*. Кроме того, на ползун 5 со стороны отброшенной стойки-направляющей действует реакция 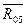 перпендикулярно направляющей. В центре масс S 4 звена 4 вертикально вниз приложена сила тяжести
перпендикулярно направляющей. В центре масс S 4 звена 4 вертикально вниз приложена сила тяжести 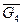 . Также к этому звену приложены нормальная
. Также к этому звену приложены нормальная  вдоль звена и тангенциальная
вдоль звена и тангенциальная  перпендикулярно звену составляющие реакции
перпендикулярно звену составляющие реакции  , учитывающей влияние отброшенного звена 3 на звено на 4**.
, учитывающей влияние отброшенного звена 3 на звено на 4**. +
+  +
+  +
+  +(
+(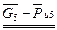 ) = 0.
) = 0.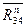 и
и  .
.
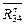 ,
,  и (
и ( ). Затем через начало вектора
). Затем через начало вектора 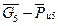 ). Направление реакции
). Направление реакции 
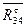 , то получим полную реакцию
, то получим полную реакцию  и (
и ( ) прикладываем реакцию
) прикладываем реакцию  . Её направление неизвестно, поэтому она нарисована пунктиром*. Реакция R45 находится из плана сил рис. 19, б, построенного по уравнению равновесия для пятого звена:
. Её направление неизвестно, поэтому она нарисована пунктиром*. Реакция R45 находится из плана сил рис. 19, б, построенного по уравнению равновесия для пятого звена:  ) +
) +  = 0. Откладываем один за другим известные вектора
= 0. Откладываем один за другим известные вектора  ), соединяем конец вектора
), соединяем конец вектора 


