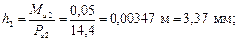РЫЧАЖНОГО МЕХАНИЗМА В ХОЛОСТОМ ХОДЕ

 

Вычерчиваем схему механизма в расчетном положении, например, в 11-м (рис. 17) и прикладываем внешние силы и моменты:

б

а

Рис. 17. Расчетная схема механизма при холостом ходе (а)

и план ускорений (б)

 

силы тяжести, силы инерции и инерционные моменты. Рекомендуется инерционную силу и инерционный момент учитывать только силой инерции, приложенной в центре качания звена (см. раздел 2 пункт 5 стр. 7). Тогда из всех сил тяжести и инерции можно выбрать максимальную силу и далее учитывать только те силы, которые составляют от этой максимальной силы более 5%.

Пусть известны (даны) силы тяжести: G ₂ = 70 Н, G ₃ = 90 Н, G ₄ = 35 Н, G ₅ = 150 Н. Вычисляем величину сил инерции по формуле Р_u = m × a_s, где m – масса звена (m = G / g, где g = 9,81 м/с² – ускорение свободного падения), a_s – ускорение центра масс звена (определяем по плану ускорений для данного положения механизма).

Р_{u 2} = m ₂ a_{s 2} = = 14,4 Н;

Р_{u 3} = m ₃ a_{s 3} = = 8,7 Н;

Р_{u 4} = m ₄ a_{s 4} = = 3,25 Н;

Р_{u 5} = m ₅ a_{s 5} = = 13,9 Н.

Вычисляем величину инерционных моментов по формуле М_u = I_s ε, где I_s - момент инерции звена (он либо задан, либо равен I_s = ml ²/12, где l - длина звена), ε - угловое ускорение звена в данном положении механизма (ε = a ^τ/ l, где a ^τ - тангенциальная составляющая относительного ускорения точек звена, определяемая по плану ускорений):

М_{u 2} = I_{s 2}ε₂ = 0,05 Н×м;

М_{u 3} = I_{s 3}ε₃ = 0,095 Н×м;

М_{u 4} = I_{s 4}ε₄ = 0,009 Н×м.

Вычисляем плечи смещения результирующих сил инерции относительно центра масс:

 

Сравнивая значения сил тяжести и сил инерции, получаем, что максимальная сила – это G ₅ = 150 Н и 5% от неё составляет 7,5 Н. Поэтому далее будем учитывать все силы тяжести, приложенные в центре масс звеньев, и все силы инерции, кроме Р_u4 , приложенные в центрах качания звеньев. Так же, за малостью, не будем учитывать инерционный момент М_{и 4}. Кроме того, если плечо смещения в масштабе длин чертежа не превысит 1 мм, то это плечо также учитывать не будем и соответствующую силу инерции приложим в центр масс звена.