Структурная группа звеньев 2-3. Рисуем группу (рис. 20) с приложенными внешними силами, а влияние отброшенных связей (звеньев) в точках В и D заменяем реакциями и
Рисуем группу (рис. 20) с приложенными внешними силами, а влияние отброшенных связей (звеньев) в точках В и D заменяем реакциями Запишем первое уравнение равновесия структурной группы: векторная сумма всех сил должна быть равна нулю:
В этом уравнении четыре величины неизвестных реакций. Две из них – тангенциальные составляющие – находим из второго условия равновесия: сума моментов всех сил относительно внутренней кинематической пары отдельно для каждого из звеньев должна быть равна нулю. Затем находим нормальные составляющие реакций из плана сил, построенного для всей структурной группы. Итак, для второго звена: Σ Мс = 0; откуда
Рис. 20. Расчетная схема структурной группы звеньев 2-3
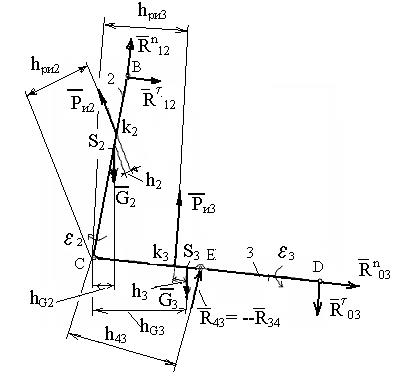
Для третьего звена: Σ Мс = 0 R 03τ CD – R 43 h 43 + G 3 hG 3 – Pu 3 hPu 3 = 0,
откуда R 03τ = В этих уравнениях плечи сил можно брать с чертежа без учета масштаба длин, так как он все равно бы сократился. Будем считать, что величины реакций R 12τ и R 03τ получили со знаком плюс. Значит, угадали правильное направление этих реакций. Если бы получили знак минус, то при построении плана сил направление соответствующей реакции нужно было бы рисовать противоположное.
Точка пересечения этих линий ограничивает величину соответствующих реакций. При построении плана сил известные вектора можно откладывать в любом порядке. Но, как уже было отмечено, лучше, чтобы вначале были отложены все силы, приложенные к одному звену, а затем все силы, приложенные к другому. Кроме того, желательно начинать построение уже с найденной тангенциальной составляющей одного звена группы, а заканчивать тангенциальной составляющей другого звена группы. В этом случае на этом же плане сил можно показать, во-первых, полную реакцию в соответствующей кинематической паре и, во-вторых, полную реакцию во внутренней кинематической паре. Так, на рис. 21 пунктиром показана реакция
Таким образом, найдены реакции во всех кинематических парах структурной группы звеньев 2-3. Теперь в соответствии с порядком силового расчета и формулой строения механизма, следует перейти к анализу механизма 1-го класса.
|

 и
и  , каждая из которых в виде двух составляющих: нормальной
, каждая из которых в виде двух составляющих: нормальной  вдоль звена и тангенциальной
вдоль звена и тангенциальной 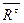 перпендикулярно звену. Реакция в точке Е
перпендикулярно звену. Реакция в точке Е  , учитывающая влияние отброшенного звена 4, считается уже внешней силой, найденной при силовом анализе предыдущей структурной группы.
, учитывающая влияние отброшенного звена 4, считается уже внешней силой, найденной при силовом анализе предыдущей структурной группы. +
+  +
+ 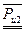 +
+  +
+  +
+  +
+  +
+  +
+  = 0.
= 0. ВС +
ВС +  hG 2 –
hG 2 –  hPu 2 =0,
hPu 2 =0,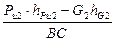 .
.
 .
. У нас остались две неизвестные величины нормальных составляющих реакций во внешних кинематических парах. Их находим из плана сил. Строим его (рис. 21), откладываем последовательно все известные силы, приложенные вначале к одному звену, например 2-му, а затем все силы, приложенные к другому, например 3-му, т.е. последовательно откладываем вектора
У нас остались две неизвестные величины нормальных составляющих реакций во внешних кинематических парах. Их находим из плана сил. Строим его (рис. 21), откладываем последовательно все известные силы, приложенные вначале к одному звену, например 2-му, а затем все силы, приложенные к другому, например 3-му, т.е. последовательно откладываем вектора  ,
,  ,
,  ,
,  ,
,  ,
,  . После этого через начало вектора
. После этого через начало вектора  параллельно звену ВС, а через конец вектора
параллельно звену ВС, а через конец вектора  параллельно звену СD.
параллельно звену СD. как сумма векторов
как сумма векторов  как векторная сумма сил, приложенных ко второму звену. Последнее следует из условия равновесия второго звена:
как векторная сумма сил, приложенных ко второму звену. Последнее следует из условия равновесия второго звена: +
+  +
+  = 0.
= 0.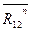 ,
,  ,
, 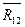 ,
, 



