Ø Определения. 1. Проекцией данной точки (А, черт. 3) на какую-нибудь плоскость (V) называется та точка (а) этой плоскости, в которой с ней пересекается прямая (AM), проведенная из данной точки параллельно заданному направлению (ху).
Прямая AM называется в таком случае проектирующей прямой, а плоскость V — плоскостью проекций. Если проектирующая прямая перпендикулярна к плоскости проекций, то проекция называется прямоугольной или ортогональной, в противном случае — косоугольной.

Черт. 3
2. Проекцией какой-нибудь фигуры на данную плоскость называется геометрическое место проекций всех точек этой фигуры на эту плоскость.
Ø Свойства проекции прямых линий.
| Свойства
| Наглядное изображение
|
| Проекция прямой (АВ, черт. 3) на любую плоскость (V) есть прямая (ab).
| Черт. 3
|
| Если прямая параллельна плоскости проекций, то ее проекция параллельна самой прямой.
|  Черт. 4 Черт. 4
|
| Отрезок прямой, параллельной плоскости проекций, проектируется на нее в натуральную величину.
|
Черт.4
|
| Отрезок прямой, непараллельной плоскости проекций, проектируется на нее вообще не в натуральную величину.
|  Черт. 5 Черт. 5
|
| Если отрезок (АВ, черт. 6) разделен на несколько частей (АС, СВ,...), то и проекция его разделится на столько же частей (ас, cb,...), причем части проекции пропорциональны соответствующим частям отрезка.
| 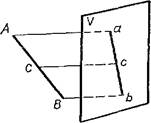 Черт. 6 Черт. 6
|
| Проекции параллельных прямых параллельны (черт. 7).
| 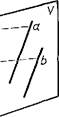 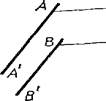 Черт. 7 Черт. 7
|
| Проекции пересекающихся прямых пересекаются между собой.
|
|
Сравнение проекций трех родов.
Сравнивая между собой проекции: ортогональные, косоугольные и перспективные, мы видим, что каждая из них обладает своими достоинствами и своими недостатками.
| Проектирование
| Плюсы
| Минусы
|
|
Ортогональное
| давая план, фасад, а иногда и профиль изображаемого предмета, позволяет безошибочно судить о расположении в пространстве всех частей его и об их относительном размере;
| составить себе по ортогональным проекциям ясное понятие о том, как этот предмет представлялся бы глазу, часто весьма затруднительно (иногда чертеж бывает очень сложный);
|
|
Перспективное
| наоборот, дает вполне наглядное зрительное представление о предмете;
| но не указывает точных размеров его частей;
|
|
Косоугольное
| уподобляясь перспективному, дает более наглядное, чем при ортогональном проектировании, представление о виде предмета и до некоторой степени позволяет судить также и о размерах его частей (если известен масштаб «сокращения»).
|
|
Ортогональные проекции имеют весьма большое значение в тех случаях, когда по данному чертежу требуется изготовить самый предмет (например, при постройке домов, мостов, машин и т. п.). Перспективное черчение употребительно в тех случаях, когда желательно, чтобы зритель, смотрящий на картину, сразу составил себе ясное представление об изображенном предмете; им пользуются в рисовании и живописи. Косоугольное проектирование полезно тогда, когда при помощи не очень сложных чертежей желают дать довольно наглядное представление о предмете и в то же время указать чертежом (хотя и приблизительно) на относительные размеры его частей. Такими чертежами иллюстрируются, например, книги по геометрии. Решим следующие задачи:
 Задача 1. Изобразить на плоскости α данный четырехугольник, используя центральную проекцию.
Задача 1. Изобразить на плоскости α данный четырехугольник, используя центральную проекцию.
 Задача 2. Изобразить на плоскости α данный четырехугольник, используя косоугольную проекцию.
Задача 2. Изобразить на плоскости α данный четырехугольник, используя косоугольную проекцию.
 Задача 3. Изобразить на плоскости α данный четырехугольник, используя прямоугольную проекцию.
Задача 3. Изобразить на плоскости α данный четырехугольник, используя прямоугольную проекцию.


 Черт. 4
Черт. 4
 Черт. 5
Черт. 5
 Черт. 6
Черт. 6

 Черт. 7
Черт. 7
 Задача 1. Изобразить на плоскости α данный четырехугольник, используя центральную проекцию.
Задача 1. Изобразить на плоскости α данный четырехугольник, используя центральную проекцию. Задача 2. Изобразить на плоскости α данный четырехугольник, используя косоугольную проекцию.
Задача 2. Изобразить на плоскости α данный четырехугольник, используя косоугольную проекцию. Задача 3. Изобразить на плоскости α данный четырехугольник, используя прямоугольную проекцию.
Задача 3. Изобразить на плоскости α данный четырехугольник, используя прямоугольную проекцию.


